图像分类

目标：所谓图像分类问题，就是已有固定的分类标签集合，然后对于输入的图像，从分类标签集合中找出一个分类标签，最后把分类标签分配给该输入图像。虽然看起来挺简单的，但这可是计算机视觉领域的核心问题之一，并且有着各种各样的实际应用。在后面的课程中，我们可以看到计算机视觉领域中很多看似不同的问题（比如物体检测和分割），都可以被归结为图像分类问题。

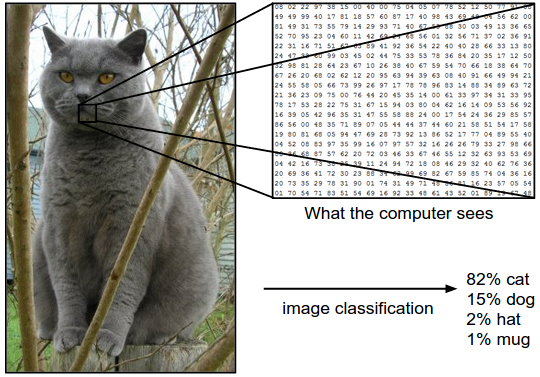
preview

图像分类流程。在课程视频中已经学习过，图像分类就是输入一个元素为像素值的数组，然后给它分配一个分类标签。完整流程如下：

  • 输入：输入是包含N个图像的集合，每个图像的标签是K种分类标签中的一种。这个集合称为训练集。
  • 学习：这一步的任务是使用训练集来学习每个类到底长什么样。一般该步骤叫做训练分类器或者学习一个模型。
  • 评价：让分类器来预测它未曾见过的图像的分类标签，并以此来评价分类器的质量。我们会把分类器预测的标签和图像真正的分类标签对比。毫无疑问，分类器预测的分类标签和图像真正的分类标签如果一致，那就是好事，这样的情况越多越好。

K-nearest算法（KNN）

需要样本尽量高密度占据样本空间

曼哈顿距离（L1）

[公式]

适合样本空间向量属性已知的情况，虽坐标轴变化值不同

欧式距离（L2）

[公式]

适合样本向量为一般的通用向量

超参数选择

选取超参数的正确方法是：将原始训练集分为训练集和验证集，我们在验证集上尝试不同的超参数，最后保留表现最好那个。如果训练数据量不够，使用交叉验证方法，它能帮助我们在选取最优超参数的时候减少噪声。

交叉验证

有时候，训练集数量较小（因此验证集的数量更小），可以将训练集平均分成5份，其中4份用来训练，1份用来验证。然后我们循环着取其中4份来训练，其中1份来验证，最后取所有5次验证结果的平均值作为算法验证结果。

线性分类

[公式]

img

图像数据预处理

对输入的特征作归一化(normalization),对每个特征减去平均值去中心化，然后将数值分布区间变为[-1,1]，称为零均值中心化。

损失函数

多类支持向量机损失 Multiclass Support Vector Machine Loss

针对第j个类别的得分就是第j个元素：[公式]。针对第i个数据的多类SVM的损失函数定义如下：

[公式]

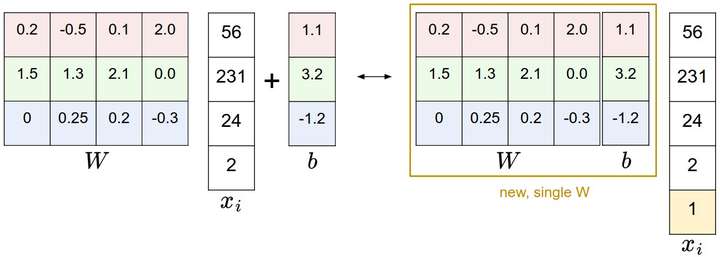
在线性分类模型中，我们面对的是线性评分函数（[公式]），可以将损失函数的公式稍微改写一下：

[公式]

其中$w_j$是权重$W$的第j行，被变形为列向量。然而，一旦开始考虑更复杂的评分函数$f$公式，这样做就不是必须的了。

$max(0,-)$称为折叶损失函数，但也会有平方折叶损失SVM，如何选择这两种可以通过交叉验证来进行选择。

损失函数的正则化(Regularization)

为了防止过拟合，需要对损失函数进行正则化操作。不是为了拟合数据而是为了减轻模型的复杂度。

正则项

$\lambda R(W)$

超参数$\lambda$用来平衡Data loss项和Regularization

常见的正则化

批量归一化，随机深度

L1 更倾向于稀疏解

L2 更倾向于鲁棒性更强的解（鲁棒性：鲁棒性是指异常样本对于算法的整体性能影响不大）

多项式逻辑斯蒂克损失(softmax loss)

在Softmax分类器中，函数映射[公式]保持不变，但将这些评分值视为每个分类的未归一化的对数概率，并且将折叶损失（hinge loss）替换为交叉熵损失（cross-entropy loss）。公式如下：

[公式] 或者 [公式]

在上式中，使用$f_j$来表示分类评分向量$f$中的第j个元素。和之前一样，整个数据集的损失值是数据集中所有样本数据的损失值$L_i$的均值与正则化损失$R(W)$之和。其中函数$f_j(z)=\frac{e^zj}{\sum_ke^zk}$被称作softmax 函数：其输入值是一个向量，向量中元素为任意实数的评分值（$z$中的)，函数对

其进行压缩，输出一个向量，其中每个元

素值在0到1之间，且所有元素之和为1。

优化

梯度

​ 在权重空间中找到一个方向，沿着该方向能降低损失函数的损失值。其实不需要随机寻找方向，因为可以直接计算出最好的方向，这就是从数学上计算出最陡峭的方向。这个方向就是损失函数的梯度（gradient）

梯度下降

1
2
3
4
5
# 普通的梯度下降

while True:
  weights_grad = evaluate_gradient(loss_fun, data, weights)
  weights += - step_size * weights_grad # 进行梯度更新
1
2
3
4
5
6
7
# 普通的小批量数据梯度下降
#可以减少运算成本

while True:
  data_batch = sample_training_data(data, 256) # 256个数据
  weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
  weights += - step_size * weights_grad # 参数更新