【本文转载自Github,对其知识点进行补充】

深度学习

神经网络中的Epoch、Iteration、Batchsize

神经网络中epoch与iteration是不相等的

  • batchsize：中文翻译为批大小（批尺寸）。在深度学习中，一般采用SGD训练，即每次训练在训练集中取batchsize个样本训练；

  • iteration：中文翻译为迭代，1个iteration等于使用batchsize个样本训练一次；一个迭代 = 一个正向通过+一个反向通过

  • epoch：迭代次数，1个epoch等于使用训练集中的全部样本训练一次；一个epoch = 所有训练样本的一个正向传递和一个反向传递

举个例子，训练集有1000个样本，batchsize=10，那么：训练完整个样本集需要：100次iteration，1次epoch。

img

参考资料

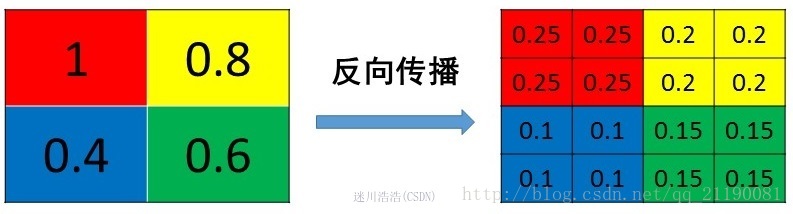
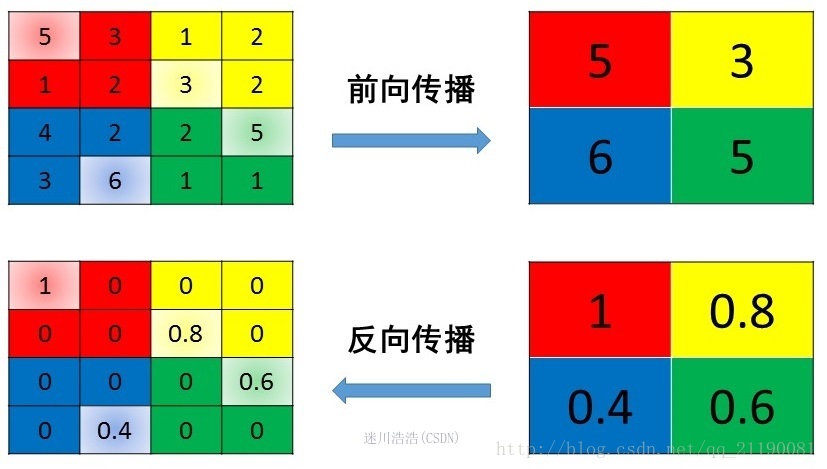
反向传播（BP）

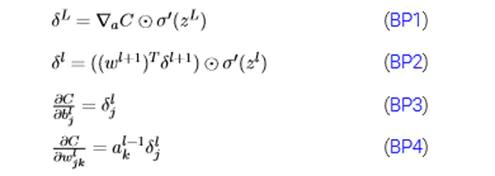
参考资料

CNN本质和优势

局部卷积（提取局部特征）

权值共享（降低训练难度）

Pooling（降维，将低层次组合为高层次的特征，保留主要特征，减少下一层的参数和计算量，防止过拟合）

多层次结构

鞍点的定义和特点？

鞍点的定义

一个不是局部最小值的驻点（一阶导数为0的点）称为鞍点。数学含义是： 目标函数在此点上的梯度（一阶导数）值为 0， 但从改点出发的一个方向是函数的极大值点，而在另一个方向是函数的极小值点。

极值点、驻点、鞍点、拐点

神经网络数据预处理方法有哪些？

1.3数据预处理

神经网络怎样进行参数初始化？

1.3数据预处理

卷积

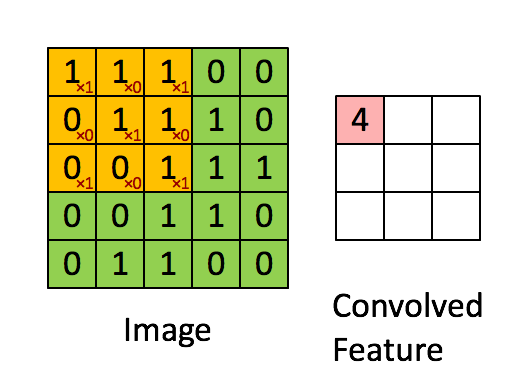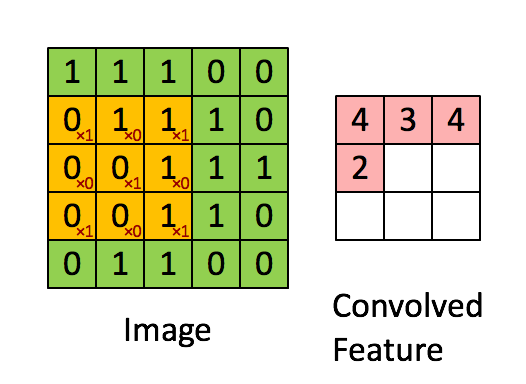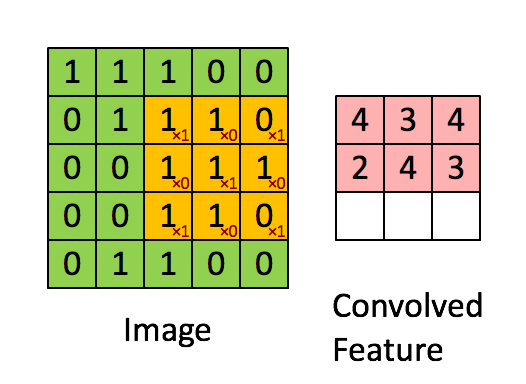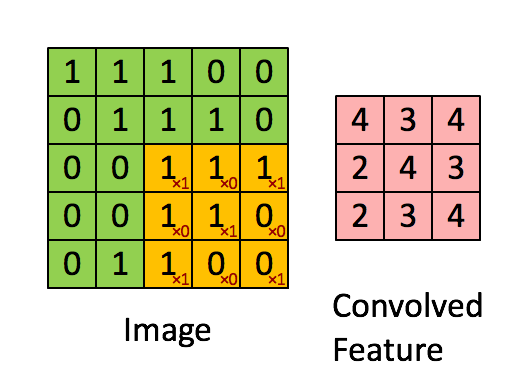
卷积的可以看作是滤波器

参考资料

卷积的反向传播过程

  • [ ] TODO

参考资料

CNN 模型所需的计算力（flops）和参数（parameters）数量是怎么计算的？

对于一个卷积层，假设其大小为 $hwcn$ （其中c为input channel, n为output channel），输出的feature map尺寸为 $HW$ ，则该卷积层的

  • paras =

  • FLOPs =

  • [ ] TODO

参考资料

池化（Pooling）

平均池化（Mean Pooling）

mean pooling的前向传播就是把一个patch中的值求取平均来做pooling，那么反向传播的过程也就是把某个元素的梯度等分为n份分配给前一层，这样就保证池化前后的梯度（残差）之和保持不变，还是比较理解的，图示如下

最大池化（Max Pooling）

max pooling也要满足梯度之和不变的原则，max pooling的前向传播是把patch中最大的值传递给后一层，而其他像素的值直接被舍弃掉。那么反向传播也就是把梯度直接传给前一层某一个像素，而其他像素不接受梯度，也就是为0。所以max pooling操作和mean pooling操作不同点在于需要记录下池化操作时到底哪个像素的值是最大，也就是max id，这个可以看caffe源码的pooling_layer.cpp，下面是caffe框架max pooling部分的源码

1
2
3
4
5
6
7
8
9
10
// If max pooling, we will initialize the vector index part.

if (this->layer_param_.pooling_param().pool() == PoolingParameter_PoolMethod_MAX && top.size() == 1)

{

    max_idx_.Reshape(bottom[0]->num(), channels_, pooled_height_,pooled_width_);

  }

参考资料

池化层怎么接收后面传过来的损失？

Relu函数的导数计算

池化层的反向传播

池化层没有激活函数，可以将池化看成用线性激活函数，所以直接做一次逆池化的操作，将池化后的单元映射到原来特征图的位置。

感受野

在卷积神经网络中，感受野的定义是 卷积神经网络每一层输出的特征图（feature map）上的像素点在原始图像上映射的区域大小。

感受野计算

参考资料

卷积神经网络的感受野

(N-1)_RF = f(N_RF, stride, kernel) = (N_RF - 1) * stride + kernel

其中，RF是感受野。N_RF和RF有点像，N代表 neighbour，指的是第n层的 a feature在n-1层的RF，记住N_RF只是一个中间变量，不要和RF混淆。 stride是步长，ksize是卷积核大小。

这个公式就是卷积之后特征图计算(N-ksize)/stride+1的逆公式

与padding没有关系，感受野只是表示两者的映射关系，与原始图的大小无关！

参考资料

权重初始化方法

权重初始化太小会造成网络崩溃，权重太大网络饱和，导致梯度消失。

Xavier

1
w = np.random.randn(fan_in, fan_out) / np.sqrt(fan_in)

Kaiming初始化

如果使用ReLU激活函数，会造成一半左右的神经元消失

在权重初始化的时候w = np.random.randn(fan_in, fan_out) / np.sqrt(fan_in / 2)

正则化方法

  1. 参数范数惩罚

    深度学习中只对网络权重θ添加约束，对偏置项不加约束。主要原因是偏置项一般需要较少的数据就能精确的拟合，不对其正则化也不会引起太大的方差。另外，正则化偏置参数反而可能会引起显著的欠拟合。

  2. L2参数正则化

  3. L1参数正则化

  4. L1正则化和L2正则化的区别

    L1为曼哈顿距离

    L2为欧式距离

    • 损失函数

    L1(LAD绝对值损失函数)和L2(LSE最小平方误差)都可以用作损失函数，LAE的鲁棒性更强，因为LSE会将误差放大，对样本更加敏感，导致模型会为了拟合一些异常样本进行调整会牺牲一些正常样本的训练效果。

    • 正则化

    L1正则化更倾向于稀疏解，常用来做特征选择，一定程度上可以防止过拟合。

    L2正则化主要是用来防止模型过拟合，直观上理解是对较大的参数进行惩罚。

    L1正则化输出稀疏，鲁棒性更强，但可能解不唯一，L2正则化有唯一解，计算相对容易

  5. 数据集增强

    利用一些数据增广操作

  6. 噪音的鲁棒性

  7. 向输出目标注入噪声

  8. 半监督学习

  9. 多任务学习

  10. 提前终止

  11. 参数绑定和共享

  12. 稀疏表示

  13. 集成化方法

    模型ensemble

参考资料

Batch Normalization（BN）

BN 原理

为什么需要BN？

传入一个模型的数据如果是独立同分布的，那么会加速模型的拟合以及简化训练等。因此需要对传入模型的数据进行白化

白化一般有两个目的：

  1. 去除特征之间的相关性（独立）
  2. 使所有的特征具有相同的均值和方差（同分布）

典型的白化方法为PCA

但是白化的计算成本会很高，并且会改变分布，导致失去原有数据的表达能力，所以提出了Batch Normalization

Internal Covariate Shift（ICS）

在深层神经网络中经过每一层之后的数据分布都会发生变化，通过叠加高层的输入分布变化会非常剧烈，这就使得高层需要不断去重新适应底层的参数更新所以会导致网络训练缓慢难以训练，为了训练好模型会非常谨慎的设定学习率，初始化权重等操作。

大家都知道在统计机器学习中的一个经典假设是“源空间（source domain）和目标空间（target domain）的数据分布（distribution）是一致的”。如果不一致，那么就出现了新的机器学习问题，如 transfer learning / domain adaptation 等。而 covariate shift 就是分布不一致假设之下的一个分支问题，它是指源空间和目标空间的条件概率是一致的，但是其边缘概率不同，即：对所有

[公式],[公式]

但是[公式]大家细想便会发现，的确，对于神经网络的各层输出，由于它们经过了层内操作作用，其分布显然与各层对应的输入信号分布不同，而且差异会随着网络深度增大而增大，可是它们所能“指示”的样本标记（label）仍然是不变的，这便符合了covariate shift的定义。由于是对层间信号的分析，也即是“internal”的来由。

带来的问题

1）上层网络需要不停调整来适应输入数据分布的变化，导致网络学习速度的降低

2）网络的训练过程容易陷入梯度饱和区，减缓网络收敛速度

3）每层的更新都会影响到其它层，因此每层的参数更新策略需要尽可能的谨慎。

具体实现

1.将每个特征进行normalization，让每个特征成为均值为0方差为1分布。

2.利用参数进行线性变换操作，让数据恢复表达能力

BN的作用

（1）BN使得网络中每层输入数据的分布相对稳定，加速模型学习速度

（2）BN使得模型对网络中的参数不那么敏感，简化调参过程，使得网络学习更加稳定

（3）BN允许网络使用饱和性激活函数（例如sigmoid，tanh等），缓解梯度消失问题

（4）BN具有一定的正则化效果

参考资料

手写 BN

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import numpy as np

def Batchnorm(x, gamma, beta, bn_param):

    # x_shape:[B, C, H, W]
    running_mean = bn_param['running_mean']
    running_var = bn_param['running_var']
    results = 0.
    eps = 1e-5

    x_mean = np.mean(x, axis=(0, 2, 3), keepdims=True)
    x_var = np.var(x, axis=(0, 2, 3), keepdims=True0)
    x_normalized = (x - x_mean) / np.sqrt(x_var + eps)
    results = gamma * x_normalized + beta

    # 因为在测试时是单个图片测试，这里保留训练时的均值和方差，用在后面测试时用
    running_mean = momentum * running_mean + (1 - momentum) * x_mean
    running_var = momentum * running_var + (1 - momentum) * x_var

    bn_param['running_mean'] = running_mean
    bn_param['running_var'] = running_var

    return results, bn_param

BN 可以防止过拟合么？为什么

在Batch Normalization中，由于我们使用mini-batch的均值与方差作为对整体训练样本均值与方差的估计，尽管每一个batch中的数据都是从总体样本中抽样得到，但不同mini-batch的均值与方差会有所不同，这就为网络的学习过程中增加了随机噪音，与Dropout通过关闭神经元给网络训练带来噪音类似，在一定程度上对模型起到了正则化的效果。

另外，原作者通过也证明了网络加入BN后，可以丢弃Dropout，模型也同样具有很好的泛化效果。

BN 有哪些参数？

首先对原始数据进行去均值除方差的操作编程均值为0方差为1的分布

再用可学习的参数g，b将输入的数据变成均值为b，方差为g2的分布

加入g,b参数的原因是保证模型的表达能力不因规范化而下降。可以让上层的网络利用下层学习的结果进行学习。

在旧参数中，X的均值取决于下层神经网络的复杂关联；但在新参数中， Y 的均值仅由 b来确定，去除了与下层计算的密切耦合。新参数很容易通过梯度下降来学习，简化了神经网络的训练。

BN 的反向传播推导

我们可以看到，经过BN操作以后，权重的缩放值会被“抹去”，因此保证了输入数据分布稳定在一定范围内。另外，权重的缩放并不会影响到对$u$的梯度计算；并且当权重越大时，即$a$越大， $\frac{1}{a}$越小，意味着权重 $W$的梯度反而越小，这样BN就保证了梯度不会依赖于参数的scale，使得参数的更新处在更加稳定的状态。

因此，在使用Batch Normalization之后，抑制了参数微小变化随着网络层数加深被放大的问题，使得网络对参数大小的适应能力更强，此时我们可以设置较大的学习率而不用过于担心模型divergence的风险。

BN 在训练和测试的区别？

训练时$\mu$和$\sigma$是从mini_batch的样本求得的均值和方差

在测试时,使用在训练时BN保留的每组mini-batch训练数据在网络中每一层的均值和方差，即用整个样本的均值和方差来对test数据进行归一化。

Weight Normalization（WN）

Layer Normalization（LN）

层规范化就是针对 BN 的上述不足而提出的。与 BN 不同，LN 是一种横向的规范化，如图所示。它综合考虑一层所有维度的输入，计算该层的平均输入值和输入方差，然后用同一个规范化操作来转换各个维度的输入。

即将该层所有输入的神经元进行归一化，将所有特征一起考虑，如果特征差距过大则会降低模型的表现能力

LN中同层神经元输入拥有相同的均值和方差，不同的输入样本有不同的均值和方差

LN主要用在RNN中

1
2
3
4
5
def ln(x, b, s):
    _eps = 1e-5
    output = (x - x.mean(1)[:,None]) / tensor.sqrt((x.var(1)[:,None] + _eps))
    output = s[None, :] * output + b[None,:]
    return output

Instance Normalization（IN）

IN对输入的每个图像实例进行归一化

1
2
3
4
5
6
7
8
9
10
11
def Instancenorm(x, gamma, beta):

    # x_shape:[B, C, H, W]
    results = 0.
    eps = 1e-5

    x_mean = np.mean(x, axis=(2, 3), keepdims=True)
    x_var = np.var(x, axis=(2, 3), keepdims=True0)
    x_normalized = (x - x_mean) / np.sqrt(x_var + eps)
    results = gamma * x_normalized + beta
    return results

Group Normalization（GN）

主要是针对Batch Normalization对小batchsize效果差，GN将channel方向分group，然后每个group内做归一化，算(C//G)HW的均值，这样与batchsize无关，不受其约束。

1
2
3
4
5
6
7
8
9
10
11
12
def GroupNorm(x, gamma, beta, G=16):

    # x_shape:[B, C, H, W]
    results = 0.
    eps = 1e-5
    x = np.reshape(x, (x.shape[0], G, x.shape[1]/16, x.shape[2], x.shape[3]))

    x_mean = np.mean(x, axis=(2, 3, 4), keepdims=True)
    x_var = np.var(x, axis=(2, 3, 4), keepdims=True0)
    x_normalized = (x - x_mean) / np.sqrt(x_var + eps)
    results = gamma * x_normalized + beta
    return results

BN、LN、WN、IN和GN的区别

将输入的图像shape记为[N, C, H, W]，这几个方法主要的区别就是在，

  • batchNorm是在batch上，对NHW做归一化，对小batchsize效果不好；
  • layerNorm在通道方向上，对CHW归一化，主要对RNN作用明显；
  • instanceNorm在图像像素上，对HW做归一化，用在风格化迁移；
  • GroupNorm将channel分组，然后再做归一化；
  • SwitchableNorm是将BN、LN、IN结合，赋予权重，让网络自己去学习归一化层应该使用什么方法。

参考资料

优化算法

见神经网络优化

  • 随机梯度下降（SGD）
  • Mini-Batch
  • 动量（Momentum）
  • Nesterov 动量
  • AdaGrad
  • AdaDelta
  • RMSProp
  • Adam
  • Adamax
  • Nadam
  • AMSGrad
  • AdaBound

参考资料

梯度下降法

在梯度下降中，对于$\theta$的更新，需要计算所有的样本然后求平均.其计算得到的是一个标准梯度。因而理论上来说一次更新的幅度是比较大的。

mini-batch梯度下降法

为了克服SGD这种随机性带来的缺点，保留其优点。Mini-batch gradient descent 每次随机选择m个数据样本进行梯度下降的参数更新。m的取值可以是2，4，8，16，32，64，256等。这样做的好处是抵消了一部分随机性，又不会花费太多的时间。而且也能够在online streaming数据流的状态下使用。只要每次收集完m个数据后开始更新即可。

Batch size大，收敛速度会比较慢，因为参数每次更新所需要的样本量增加了，但是会沿着比较准确的方向进行。

随机梯度下降法（SGD）

SGD每步做什么，为什么能online learning？

  • 只对一个方向的敏感度高，会在不敏感的方向反复增减。
  • 会找到局部极小值或者鞍点(梯度为零)，在高维参数空间中，局部最小值不常见，常见的是鞍点。
  • 随机性，因为SGD使用的是minibatch(=1)，会产生噪声，如果在梯度下降时加入噪声会花费很长的时间

online learning强调的是学习是实时的，流式的，每次训练不用使用全部样本，而是以之前训练好的模型为基础，每来一个样本就更新一次模型，这种方法叫做OGD（online gradient descent）。

动量梯度下降法（Momentum）

  • 在局部最优点或者鞍点时，梯度为0，但依旧会有一个速度，能够越过这个点继续进行梯度下降。
  • 加入动量之后，噪声会被抵消，下降曲线更平滑。

参考资料

RMSprop

  • [ ] TODO

Adagrad

  • [ ] TODO

Adam

Adam算法结合了Momentum和RMSprop梯度下降法，是一种极其常见的学习算法，被证明能有效适用于不同神经网络，适用于广泛的结构。

超参数：

  • [ ] TODO

Adam 优化器的迭代公式

  • [ ] TODO

激活函数

每个激活函数（或非线性函数）的输入都是一个数字，然后对其进行某种固定的数学操作。

见2.1激活函数

参考资料

Sigmoid&Tanh

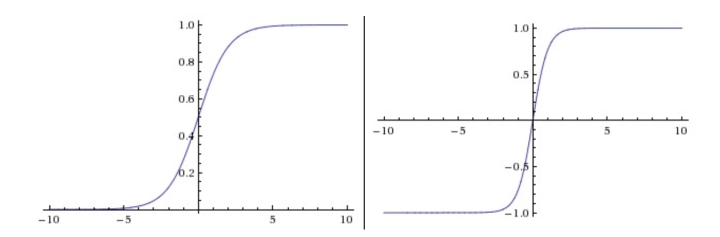
sigmod函数饱和使梯度消失，并且是非零中心的

tanh也有饱和问题，但是是零中心的

Sigmoid用作激活函数时，分类为什么要用交叉熵损失，而不用均方损失？

https://blog.csdn.net/qq_29679623/article/details/99441913

当使用sigmoid作为激活函数的时候，常用交叉熵损失函数而不用均方误差损失函数，因为它可以完美解决平方损失函数权重更新过慢的问题，具有“误差大的时候，权重更新快；误差小的时候，权重更新慢”的良好性质。

ReLU

ReLU 相关变体

ReLU 激活函数为什么比sigmoid和tanh好？

  1. 可以有效解决饱和问题带来的梯度消失问题
  2. 计算简单，导数为常数收敛速度快
  3. Relu会使一部分神经元的输出为0，这样就造成了网络的稀疏性，并且减少了参数的相互依存关系，缓解了过拟合问题的发生

ReLU 激活函数为什么能解决梯度消失问题？

从信号方面来看，即神经元同时只对输入信号的少部分选择性响应，大量信号被刻意的屏蔽了，这样可以提高学习的精度，更好更快地提取稀疏特征。当 x<0 时，relu 硬饱和，而当 x>0 时，则不存在饱和问题。ReLU 能够在 x>0 时保持梯度不衰减，从而缓解梯度消失问题。

ReLU 有哪些变体？

Leaky ReLU PReLU ELU

Dropout

Dropout 基本原理

解决过拟合和模型耗时问题，随机选择部分神经元失活

参考资料

Dropout 如何实现？

  • [ ] TODO

Drop 在训练和测试的区别

在测试的时候每个单元的参数需要乘p

损失函数（Loss）

在机器学习中，损失函数（loss function）是用来估量模型的预测值f(x)与真实值Y的不一致程度，损失函数越小，一般就代表模型的鲁棒性越好，正是损失函数指导了模型的学习。

常见的损失函数

MSE

参考

均方误差主要用于回归，不经常用于分类

使用MSE的一个缺点就是其偏导值在输出概率值接近0或者接近1的时候非常小，这可能会造成模型刚开始训练时，偏导值几乎消失。

如果假设您的输出是输入的实值函数，并且具有一定量的不可约高斯噪声，并且均值和方差恒定，那么使用MSE损失才有意义。 如果这些假设不成立（例如在分类的情况下），那么MSE亏损可能不是最好的选择。

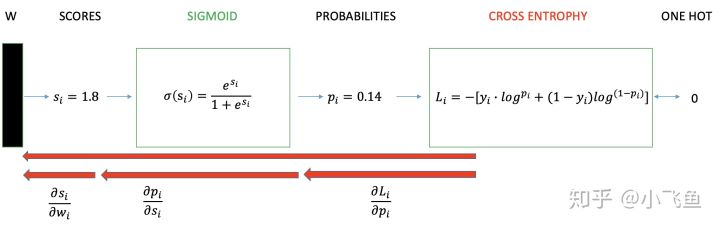
Cross Entropy Loss（CE）

log损失函数是凸函数能够求得全局最优

如果用 MSE 计算 loss， 输出的曲线是波动的，有很多局部的极值点。 即，非凸优化问题 (non-convex)

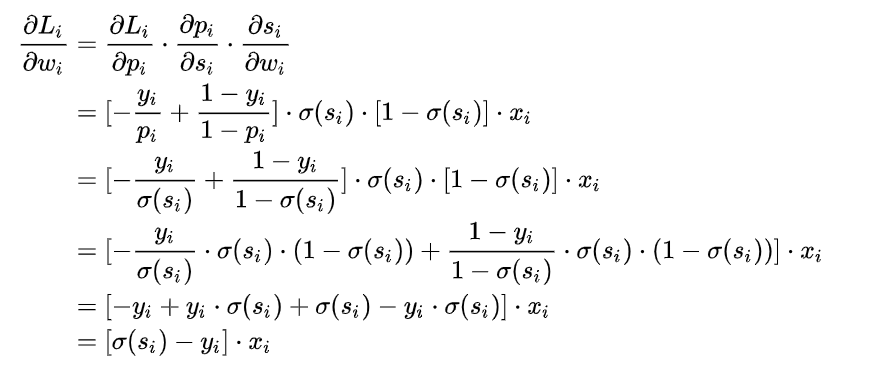
并且在反向传播时CE可以很容易的进行计算

优点

在用梯度下降法做参数更新的时候，模型学习的速度取决于两个值：一、学习率；二、偏导值。其中，学习率是我们需要设置的超参数，所以我们重点关注偏导值。从上面的式子中，我们发现，偏导值的大小取决于$x_i$ 和 $[\sigma(s)-y]$ ，我们重点关注后者，后者的大小值反映了我们模型的错误程度，该值越大，说明模型效果越差，但是该值越大同时也会使得偏导值越大，从而模型学习速度更快。所以，使用逻辑函数得到概率，并结合交叉熵当损失函数时，在模型效果差的时候学习速度比较快，在模型效果好的时候学习速度变慢。

缺点

sigmoid(softmax)+cross-entropy loss 擅长于学习类间的信息，因为它采用了类间竞争机制，它只关心对于正确标签预测概率的准确性，忽略了其他非正确标签的差异，导致学习到的特征比较散。基于这个问题的优化有很多，比如对softmax进行改进，如L-Softmax、SM-Softmax、AM-Softmax等。

pytorch中的CE Loss

pytorch中的CE Loss是由softmax-log-NLL Loss(将label对应位置的值拿出来去掉负号求均值)组合而成的

Hinge Loss

在机器学习中，hinge loss是一种损失函数，它通常用于”maximum-margin”的分类任务中，如支持向量机。数学表达式为：

Focal Loss

参考资料

Focal Loss的引入主要是为了解决难易样本数量不平衡（注意，有区别于正负样本数量不平衡）的问题。

在普通的CE loss加上一个参数$\alpha$可以解决正负样本不平衡的问题。

即减小负样本的权重

但是这样并不能解决难易样本不平衡的问题

样本可以分为四类

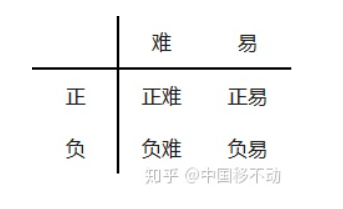
尽管 $\alpha$平衡了正负样本，但对难易样本的不平衡没有任何帮助。而实际上，目标检测中大量的候选目标都是像下图一样的易分样本。

这些样本的损失很低，但是由于数量极不平衡，易分样本的数量相对来讲太多，最终主导了总的损失。而本文的作者认为，易分样本（即，置信度高的样本）对模型的提升效果非常小，模型应该主要关注与那些难分样本（这个假设是有问题的，是GHM的主要改进对象）

一个简单的思想：把高置信度(p)样本的损失降低

实验表明$\gamma$取2, $\alpha$取0.25的时候效果最佳。

在pytorch中

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def py_sigmoid_focal_loss(pred,
                          target,
                          weight=None,
                          gamma=2.0,
                          alpha=0.25,
                          reduction='mean',
                          avg_factor=None):
    pred_sigmoid = pred.sigmoid()
    target = target.type_as(pred)
    pt = (1 - pred_sigmoid) * target + pred_sigmoid * (1 - target)
    focal_weight = (alpha * target + (1 - alpha) *
                    (1 - target)) * pt.pow(gamma)
    loss = F.binary_cross_entropy_with_logits(
        pred, target, reduction='none') * focal_weight
    loss = weight_reduce_loss(loss, weight, reduction, avg_factor)
    return loss

1*1 卷积有什么作用？

  1. 调整特征图的深度进行降维或者升维
  2. 减少参数
  3. 跨通道的信息组合，并增加了非线性特征

使用11卷积核，实现降维和升维的操作其实就是channel间信息的线性组合变化，33，64channels的卷积核前面添加一个11，28channels的卷积核，就变成了33，28channels的卷积核，原来的64个channels就可以理解为跨通道线性组合变成了28channels，这就是通道间的信息交互。因为1*1卷积核，可以在保持feature map尺度不变的（即不损失分辨率）的前提下大幅增加非线性特性（利用后接的非线性激活函数），把网络做的很deep，增加非线性特性。

AlexNet

  • 使用ReLU激活函数
  • Dropout
  • 数据增广

先给出AlexNet的一些参数和结构图：

卷积层：5层

全连接层：3层

深度：8层

参数个数：60M

神经元个数：650k

分类数目：1000类

参考资料

AlexNet

VGG

《Very Deep Convolutional Networks for Large-Scale Image Recognition》

VGG 是Oxford的Visual Geometry Group的组提出的（大家应该能看出VGG名字的由来了）。该网络是在ILSVRC 2014上的相关工作，主要工作是证明了增加网络的深度能够在一定程度上影响网络最终的性能。VGG有两种结构，分别是VGG16和VGG19，两者并没有本质上的区别，只是网络深度不一样。

VGG16相比AlexNet的一个改进是采用连续的几个3x3的卷积核代替AlexNet中的较大卷积核（11x11，7x7，5x5）。对于给定的感受野（与输出有关的输入图片的局部大小），采用堆积的小卷积核是优于采用大的卷积核，因为多层非线性层可以增加网络深度来保证学习更复杂的模式，而且代价还比较小（参数更少）。

简单来说，在VGG中，使用了3个3x3卷积核来代替7x7卷积核，使用了2个3x3卷积核来代替5*5卷积核，这样做的主要目的是在保证具有相同感知野的条件下，提升了网络的深度，在一定程度上提升了神经网络的效果。

比如，3个步长为1的3x3卷积核的一层层叠加作用可看成一个大小为7的感受野（其实就表示3个3x3连续卷积相当于一个7x7卷积），其参数总量为 3x(9xC^2) ，如果直接使用7x7卷积核，其参数总量为 49xC^2 ，这里 C 指的是输入和输出的通道数。很明显，27xC^2小于49xC^2，即减少了参数；而且3x3卷积核有利于更好地保持图像性质。

这里解释一下为什么使用2个3x3卷积核可以来代替5*5卷积核：

5x5卷积看做一个小的全连接网络在5x5区域滑动，我们可以先用一个3x3的卷积滤波器卷积，然后再用一个全连接层连接这个3x3卷积输出，这个全连接层我们也可以看做一个3x3卷积层。这样我们就可以用两个3x3卷积级联（叠加）起来代替一个 5x5卷积。

具体如下图所示：

至于为什么使用3个3x3卷积核可以来代替7*7卷积核，推导过程与上述类似，大家可以自行绘图理解。

下面是VGG网络的结构（VGG16和VGG19都在）：

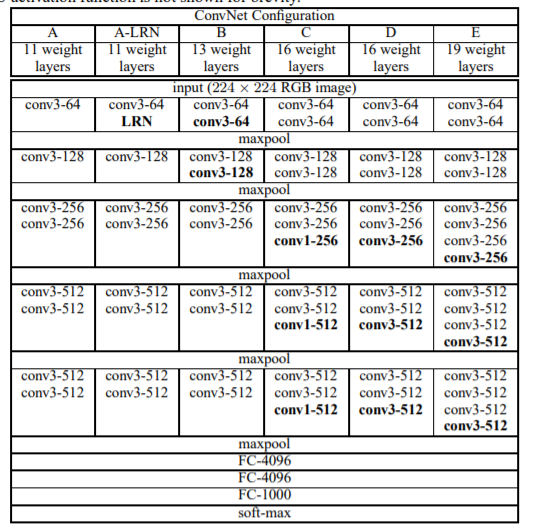
  • VGG16包含了16个隐藏层（13个卷积层和3个全连接层），如上图中的D列所示
  • VGG19包含了19个隐藏层（16个卷积层和3个全连接层），如上图中的E列所示

VGG网络的结构非常一致，从头到尾全部使用的是3x3的卷积和2x2的max pooling。

如果你想看到更加形象化的VGG网络，可以使用经典卷积神经网络（CNN）结构可视化工具来查看高清无码的VGG网络。

VGG优点：

  • VGGNet的结构非常简洁，整个网络都使用了同样大小的卷积核尺寸（3x3）和最大池化尺寸（2x2）。
  • 几个小滤波器（3x3）卷积层的组合比一个大滤波器（5x5或7x7）卷积层好：
  • 验证了通过不断加深网络结构可以提升性能。

VGG缺点：

VGG耗费更多计算资源，并且使用了更多的参数（这里不是3x3卷积的锅），导致更多的内存占用（140M）。其中绝大多数的参数都是来自于第一个全连接层。VGG可是有3个全连接层啊！

PS：有的文章称：发现这些全连接层即使被去除，对于性能也没有什么影响，这样就显著降低了参数数量。

注：很多pretrained的方法就是使用VGG的model（主要是16和19），VGG相对其他的方法，参数空间很大，最终的model有500多m，AlexNet只有200m，GoogLeNet更少，所以train一个vgg模型通常要花费更长的时间，所幸有公开的pretrained model让我们很方便的使用。

关于感受野：

假设你一层一层地重叠了3个3x3的卷积层（层与层之间有非线性激活函数）。在这个排列下，第一个卷积层中的每个神经元都对输入数据体有一个3x3的视野。

代码篇：VGG训练与测试

这里推荐两个开源库，训练请参考tensorflow-vgg，快速测试请参考VGG-in TensorFlow。

代码我就不介绍了，其实跟上述内容一致，跟着原理看code应该会很快。我快速跑了一下VGG-in TensorFlow，代码亲测可用，效果很nice，就是model下载比较烦。

贴心的Amusi已经为你准备好了VGG-in TensorFlow的测试代码、model和图像。需要的同学可以关注CVer微信公众号，后台回复：VGG。

天道酬勤，还有很多知识要学，想想都刺激~Fighting！

参考资料

ResNet

1.ResNet意义

随着网络的加深，出现了训练集准确率下降的现象，我们可以确定这不是由于Overfit过拟合造成的(过拟合的情况训练集应该准确率很高)；所以作者针对这个问题提出了一种全新的网络，叫深度残差网络，它允许网络尽可能的加深，其中引入了全新的结构如图1；
这里问大家一个问题

残差指的是什么？

其中ResNet提出了两种mapping：一种是identity mapping，指的就是图1中”弯弯的曲线”，另一种residual mapping，指的就是除了”弯弯的曲线“那部分，所以最后的输出是 y=F(x)+x
identity mapping顾名思义，就是指本身，也就是公式中的x，而residual mapping指的是“差”，也就是y−x，所以残差指的就是F(x)部分。

为什么ResNet可以解决“随着网络加深，准确率不下降”的问题？

理论上，对于“随着网络加深，准确率下降”的问题，Resnet提供了两种选择方式，也就是identity mapping和residual mapping，如果网络已经到达最优，继续加深网络，residual mapping将被push为0，只剩下identity mapping，这样理论上网络一直处于最优状态了，网络的性能也就不会随着深度增加而降低了。

可以解决网络退化问题，缓解梯度消失的问题。

2.ResNet结构

它使用了一种连接方式叫做“shortcut connection”，顾名思义，shortcut就是“抄近道”的意思，看下图我们就能大致理解：

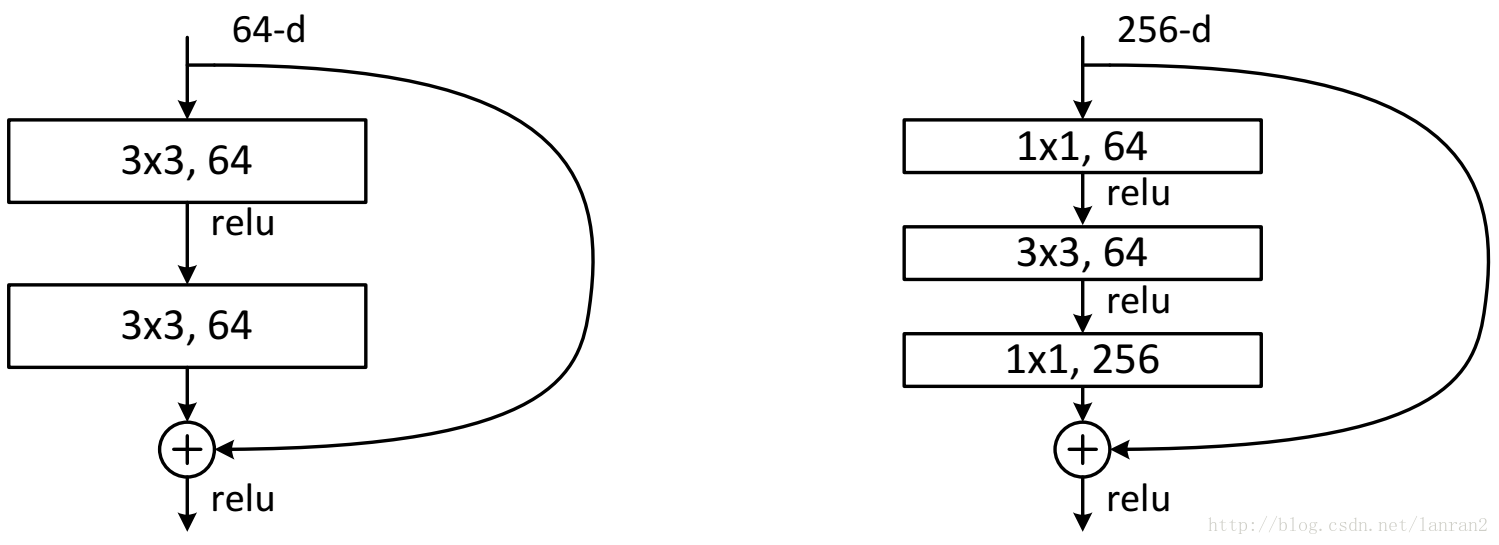
ResNet的F(x)究竟长什么样子？

参考资料

网络的深度为什么重要？

因为CNN能够提取low/mid/high-level的特征，网络的层数越多，意味着能够提取到不同level的特征越丰富。并且，越深的网络提取的特征越抽象，越具有语义信息。

为什么不能简单地增加网络层数？

  • 对于原来的网络，如果简单地增加深度，会导致梯度弥散或梯度爆炸。

  • 会出现另一个问题，就是退化问题，网络层数增加，但是在训练集上的准确率却饱和甚至下降了。这个不能解释为overfitting，因为overfit应该表现为在训练集上表现更好才对。退化问题说明了深度网络不能很简单地被很好地优化。

    F是求和前网络映射，H是从输入到求和后的网络映射。

    比如把5映射到5.1，

    那么引入残差前是F’(5)=5.1，

    引入残差后是H(5)=5.1, H(5)=F(5)+5, F(5)=0.1。

    这里的F’和F都表示网络参数映射，引入残差后的映射对输出的变化更敏感。比如原来是从5.1到5.2，映射F’的输出增加了1/51=2%，而对于残差结构从5.1到5.2，映射F是从0.1到0.2，增加了100%。明显后者输出变化对权重的调整作用更大，所以效果更好。

    残差的思想都是去掉相同的主体部分，从而突出微小的变化，看到残差网络我第一反应就是差分放大器…

    img

ResNet为什么不用Dropout?

  • [ ] TODO

参考资料

为什么 ResNet 不在一开始就使用residual block,而是使用一个7×7的卷积？

原因: 7x7卷积实际上是用来直接对输入图片降采样(early downsampling), 注意像7x7这样的大卷积核一般只出现在input layer

目的是: 尽可能保留原始图像的信息, 而不需要增加channels数.

本质上是: 多channels的非线性激活层是非常昂贵的, 在input layer用big kernel换多channels是划算的

注意一下, resnet接入residual block前pixel为56x56的layer, channels数才64, 但是同样大小的layer, 在vgg-19里已经有256个channels了.

这里要强调一下, 只有在input layer层, 也就是最靠近输入图片的那层, 才用大卷积, 原因如下:

深度学习领域, 有一种广泛的直觉，即更大的卷积更好，但更昂贵。输入层中的特征数量(224x224)是如此之小（相对于隐藏层），第一卷积可以非常大而不会大幅增加实际的权重数。如果你想在某个地方进行大卷积，第一层通常是唯一的选择。

我认为神经网络的第一层是最基本的，因为它基本上只是将数据嵌入到一个新的更大的向量空间中。ResNet在第二层之前没有开始其特征层跳过，所以看起来作者想要在开始整花里胡哨的layers之前尽可能保留图像里更多的primary features.

题外话, 同时期的GoogLeNet也在input layer用到了7x7大卷积, 所以resnet作者的灵感来源于GoogLeNet也说不定, 至于非要追问为啥这么用, 也许最直接的理由就是”深度学习就像炼丹, 因为这样网络工作得更好, 所以作者就这么用了”.

再说个有趣的例子, resnet模型是实验先于理论, 实验证明有效, 后面才陆续有人研究为啥有效, 比如The Shattered Gradients Problem: If resnets are the answer, then what is the question? 可不就是炼丹么?

参考资料

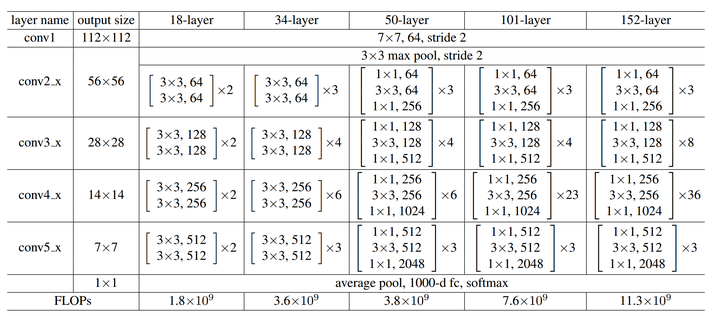
什么是Bottlenet layer？

对于常规ResNet，可以用于34层或者更少的网络中，对于Bottleneck Design的ResNet通常用于更深的如101这样的网络中，目的是减少计算和参数量（实用目的）。

ResNet如何解决梯度消失？

H(x) = F(x)+x

H’(x) = F’(x)+1

ResNet网络越来越深，准确率会不会提升？

  • [ ] TODO

ResNet v2

参考资料

ResNet v1 与 ResNet v2的区别

原始的resnet是上图中的a的模式，我们可以看到相加后需要进入ReLU做一个非线性激活，这里一个改进就是砍掉了这个非线性激活，不难理解，如果将ReLU放在原先的位置，那么残差块输出永远是非负的，这制约了模型的表达能力，因此我们需要做一些调整，我们将这个ReLU移入了残差块内部，也就是图e的模式。

ResNet v2 的 ReLU 激活函数有什么不同？

  • [ ] TODO

ResNeXt

  • [ ] TODO

参考资料

学习率如何调整

  • [ ] TODO

神经网络的深度和宽度作用

  • [ ] TODO

网络压缩与量化

  • [ ] TODO

参考资料

Batch Size

  • [ ] TODO

参考资料

BN和Dropout在训练和测试时的差别

  • [ ] TODO

参考资料

深度学习调参有哪些技巧？

参考资料

为什么深度学习中的模型基本用3x3和5x5的卷积（奇数），而不是2x2和4x4的卷积（偶数）？

参考资料

深度学习训练中是否有必要使用L1获得稀疏解?

  • [ ] TODO

参考资料

EfficientNet

  • [ ] TODO

参考资料

如何理解归一化（Normalization）对于神经网络（深度学习）的帮助？

BN最早被认为通过降低所谓Internal Covariate Shift，这种想法的出处可考至Understanding the difficulty of training deep feedforward neural networks，想必这也是batch norm作者这么设计的初衷。但是这种想法并没有过多实验支持，比如说去年NeurlPS这篇paper作者做了实验，在batch norm之后加上一些随机扰动（non-zero mean and non-unit variance，人为引入covariate shift），发现效果仍然比不加好很多。为什么放在batch norm layer之后而不是之前？因为为了证伪batch norm通过forward pass这一步降低covariate shift来提升网络训练效率的。这样说来故事就变得很有趣了，也就是说我们大概都理解一些BN对BN层之前网络噪音的好处，那么能不能研究一下它对它后面layer的影响？所以这些研究从优化的角度，有如下几种观点。

  1. BN通过修改loss function， 可以令loss的和loss的梯度均满足更强的Lipschitzness性质（即函数f满足L-Lipschitz和 [公式] -smooth，令L和 [公式] 更小，后者其实等同于f Hessian的eigenvalue小于 [公式] ，可以作为光滑程度的度量，其实吧我觉得，一般convex optimization里拿这个度量算convergence rate是神器，对于non-convex optimization，不懂鸭，paper里好像也没写的样子），这么做的好处是当步子迈得大的时候，我们可以更自信地告诉自己计算出来的梯度可以更好地近似实际的梯度，因此也不容易让优化掉进小坑里。有意思的地方来了，是不是我在某些地方插入一个1/1000 layer，把梯度的L-Lipschitz变成1/1000L-Lipschitz就能让函数优化的更好了呢？其实不是的，因为单纯除以函数会改变整个优化问题，而BN做了不仅仅rescale这件事情，还让原来近似最优的点在做完变化之后，仍然保留在原来不远的位置。这也就是这篇文章的核心论点，BN做的是问题reparametrization而不是简单的scaling。 [1]
  2. BN把优化这件事情分解成了优化参数的方向和长度两个任务，这么做呢可以解耦层与层之间的dependency因此会让curvature结构更易于优化。这篇证了convergence rate，但由于没有认真读，所以感觉没太多资格评价。[2]

归一化手段是否殊途同归？很可能是的，在[1]的3.3作者也尝试了Lp normalization，也得到了和BN差不多的效果。至于Layer norm还是weight norm，可能都可以顺着这个思路进行研究鸭，无论是通过[1]还是[2]，可能今年的paper里就见分晓了，let’s see。

  1. How Does Batch Normalization Help Optimization?
  2. Exponential convergence rates for Batch Normalization: The power of length-direction decoupling in non-convex optimization

参考资料

多标签分类怎么解决？

TODO

反卷积（deconv）/转置卷积（trans）

参考资料

空洞卷积（dilated/Atrous conv）

  • [ ] TODO

参考资料

Pooling层原理

  • [ ] TODO

depthwise卷积加速比推导

  • [ ] TODO

为什么降采用使用max pooling，而分类使用average pooling

  • [ ] TODO

max pooling如何反向传播

  • [ ] TODO

反卷积

TODO

组卷积（group convolution）

  • [ ] TODO

在说明分组卷积之前我们用一张图来体会一下一般的卷积操作。

从上图可以看出，一般的卷积会对输入数据的整体一起做卷积操作，即输入数据：H1×W1×C1；而卷积核大小为h1×w1，通道为C1，一共有C2个，然后卷积得到的输出数据就是H2×W2×C2。这里我们假设输出和输出的分辨率是不变的。主要看这个过程是一气呵成的，这对于存储器的容量提出了更高的要求。

但是分组卷积明显就没有那么多的参数。先用图片直观地感受一下分组卷积的过程。对于上面所说的同样的一个问题，分组卷积就如下图所示。

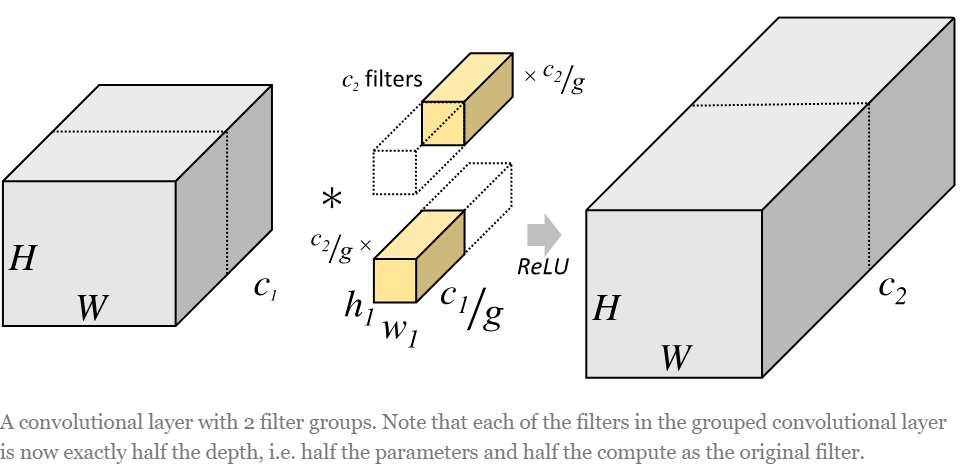
可以看到，图中将输入数据分成了2组（组数为g），需要注意的是，这种分组只是在深度上进行划分，即某几个通道编为一组，这个具体的数量由（C1/g）决定。因为输出数据的改变，相应的，卷积核也需要做出同样的改变。即每组中卷积核的深度也就变成了（C1/g），而卷积核的大小是不需要改变的，此时每组的卷积核的个数就变成了（C2/g）个，而不是原来的C2了。然后用每组的卷积核同它们对应组内的输入数据卷积，得到了输出数据以后，再用concatenate的方式组合起来，最终的输出数据的通道仍旧是C2。也就是说，分组数g决定以后，那么我们将并行的运算g个相同的卷积过程，每个过程里（每组），输入数据为H1×W1×C1/g，卷积核大小为h1×w1×C1/g，一共有C2/g个，输出数据为H2×W2×C2/g。

举个例子：

Group conv本身就极大地减少了参数。比如当输入通道为256，输出通道也为256，kernel size为3×3，不做Group conv参数为256×3×3×256。实施分组卷积时，若group为8，每个group的input channel和output channel均为32，参数为8×32×3×3×32，是原来的八分之一。而Group conv最后每一组输出的feature maps应该是以concatenate的方式组合。
Alex认为group conv的方式能够增加 filter之间的对角相关性，而且能够减少训练参数，不容易过拟合，这类似于正则的效果。

参考资料

交错组卷积（Interleaved group convolutions，IGC）

参考资料

空洞/扩张卷积（Dilated/Atrous Convolution）

Dilated convolution/Atrous convolution可以叫空洞卷积或者扩张卷积。

背景：语义分割中pooling 和 up-sampling layer层。pooling会降低图像尺寸的同时增大感受野，而up-sampling操作扩大图像尺寸，这样虽然恢复了大小，但很多细节被池化操作丢失了。

需求：能不能设计一种新的操作，不通过pooling也能有较大的感受野看到更多的信息呢？

目的：替代pooling和up-sampling运算，既增大感受野又不减小图像大小。

简述：在标准的 convolution map 里注入空洞，以此来增加 reception field。相比原来的正常convolution，dilated convolution 多了一个 hyper-parameter 称之为 dilation rate 指的是kernel的间隔数量(e.g. 正常的 convolution 是 dilatation rate 1)。

空洞卷积诞生于图像分割领域，图像输入到网络中经过CNN提取特征，再经过pooling降低图像尺度的同时增大感受野。由于图像分割是pixel−wise预测输出，所以还需要通过upsampling将变小的图像恢复到原始大小。upsampling通常是通过deconv(转置卷积)完成。因此图像分割FCN有两个关键步骤：池化操作增大感受野，upsampling操作扩大图像尺寸。这儿有个问题，就是虽然图像经过upsampling操作恢复了大小，但是很多细节还是被池化操作丢失了。那么有没有办法既增大了感受野又不减小图像大小呢？Dilated conv横空出世。

image.png

注意事项：

1.为什么不直接使用5x5或者7x7的卷积核？这不也增加了感受野么？

答：增大卷积核能增大感受野，但是只是线性增长，参考答案里的那个公式，(kernel-1)*layer，并不能达到空洞卷积的指数增长。

2.2-dilated要在1-dilated的基础上才能达到7的感受野（如上图a、b所示）

关于空洞卷积的另一种概括：

Dilated Convolution问题的引出，是因为down-sample之后的为了让input和output的尺寸一致。我们需要up-sample，但是up-sample会丢失信息。如果不采用pooling，就无需下采样和上采样步骤了。但是这样会导致kernel 的感受野变小，导致预测不精确。。如果采用大的kernel话，一来训练的参数变大。二来没有小的kernel叠加的正则作用，所以kernel size变大行不通。

由此Dilated Convolution是在不改变kernel size的条件下，增大感受野。

参考资料

转置卷积（Transposed Convolutions/deconvlution）

转置卷积（transposed Convolutions）又名反卷积（deconvolution）或是分数步长卷积（fractially straced convolutions）。反卷积（Transposed Convolution, Fractionally Strided Convolution or Deconvolution）的概念第一次出现是 Zeiler 在2010年发表的论文 Deconvolutional networks 中。

转置卷积和反卷积的区别

那什么是反卷积？从字面上理解就是卷积的逆过程。值得注意的反卷积虽然存在，但是在深度学习中并不常用。而转置卷积虽然又名反卷积，却不是真正意义上的反卷积。因为根据反卷积的数学含义，通过反卷积可以将通过卷积的输出信号，完全还原输入信号。而事实是，转置卷积只能还原shape大小，而不能还原value。你可以理解成，至少在数值方面上，转置卷积不能实现卷积操作的逆过程。所以说转置卷积与真正的反卷积有点相似，因为两者产生了相同的空间分辨率。但是又名反卷积（deconvolutions）的这种叫法是不合适的，因为它不符合反卷积的概念。

简单来说，转置矩阵就是一种上采样过程。

正常卷积过程如下，利用3x3的卷积核对4x4的输入进行卷积，输出结果为2x2

卷积过程

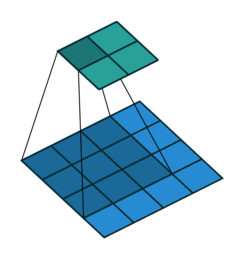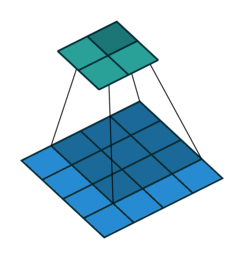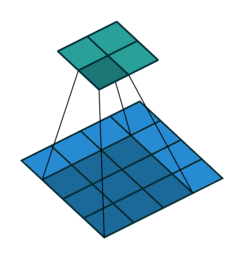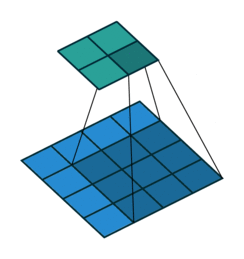
转置卷积过程如下，利用3x3的卷积核对”做了补0”的2x2输入进行卷积，输出结果为4x4。

转置卷积

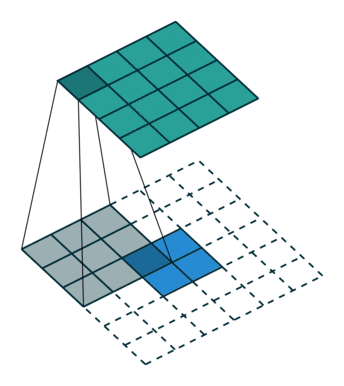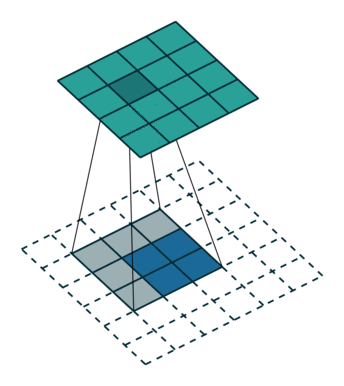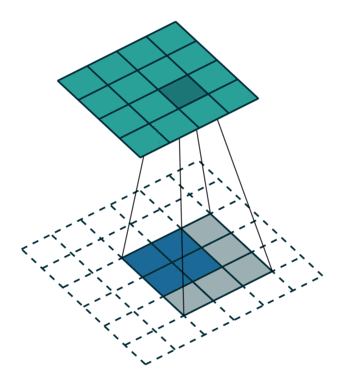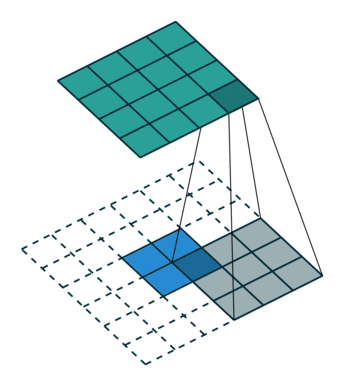
上述的卷积运算和转置卷积是”尺寸”对应的，卷积的输入大小与转置卷积的输出大小一致，分别可以看成下采样和上采样操作。

参考资料

Inception系列（V1-V4）

InceptionV1

  • [ ] TODO

InceptionV2

  • [ ] TODO

InceptionV3

  • [ ] TODO

InceptionV4

  • [ ] TODO

参考资料

DenseNet

  • [ ] TODO

为什么 DenseNet 比 ResNet 好？

  • [ ] TODO

为什么 DenseNet 比 ResNet 更耗显存？

  • [ ] TODO

SE-Net

  • [ ] TODO

Squeeze-Excitation结构是怎么实现的？

TODO

FCN

一句话概括就是：FCN将传统网络后面的全连接层换成了卷积层，这样网络输出不再是类别而是 heatmap；同时为了解决因为卷积和池化对图像尺寸的影响，提出使用上采样的方式恢复。

作者的FCN主要使用了三种技术：

  • 卷积化（Convolutional）

  • 上采样（Upsample）

  • 跳跃结构（Skip Layer）

卷积化

卷积化即是将普通的分类网络，比如VGG16，ResNet50/101等网络丢弃全连接层，换上对应的卷积层即可。

上采样

此处的上采样即是反卷积（Deconvolution）。当然关于这个名字不同框架不同，Caffe和Kera里叫Deconvolution，而tensorflow里叫conv_transpose。CS231n这门课中说，叫conv_transpose更为合适。

众所诸知，普通的池化（为什么这儿是普通的池化请看后文）会缩小图片的尺寸，比如VGG16 五次池化后图片被缩小了32倍。为了得到和原图等大的分割图，我们需要上采样/反卷积。

反卷积和卷积类似，都是相乘相加的运算。只不过后者是多对一，前者是一对多。而反卷积的前向和后向传播，只用颠倒卷积的前后向传播即可。所以无论优化还是后向传播算法都是没有问题。

跳跃结构（Skip Layers）

（这个奇怪的名字是我翻译的，好像一般叫忽略连接结构）这个结构的作用就在于优化结果，因为如果将全卷积之后的结果直接上采样得到的结果是很粗糙的，所以作者将不同池化层的结果进行上采样之后来优化输出。

上采样获得与输入一样的尺寸
文章采用的网络经过5次卷积+池化后，图像尺寸依次缩小了 2、4、8、16、32倍，对最后一层做32倍上采样，就可以得到与原图一样的大小

作者发现，仅对第5层做32倍反卷积（deconvolution），得到的结果不太精确。于是将第 4 层和第 3 层的输出也依次反卷积（图５）

参考资料

【总结】图像语义分割之FCN和CRF

图像语义分割（1）- FCN

全卷积网络 FCN 详解

U-Net

本文介绍一种编码器-解码器结构。编码器逐渐减少池化层的空间维度，解码器逐步修复物体的细节和空间维度。编码器和解码器之间通常存在快捷连接，因此能帮助解码器更好地修复目标的细节。U-Net 是这种方法中最常用的结构。

fcn(fully convolutional natwork)的思想是：修改一个普通的逐层收缩的网络，用上采样(up sampling)(？？反卷积)操作代替网络后部的池化(pooling)操作。因此，这些层增加了输出的分辨率。为了使用局部的信息，在网络收缩过程（路径）中产生的高分辨率特征(high resolution features) ，被连接到了修改后网络的上采样的结果上。在此之后，一个卷积层基于这些信息综合得到更精确的结果。

与fcn(fully convolutional natwork)不同的是，我们的网络在上采样部分依然有大量的特征通道(feature channels)，这使得网络可以将环境信息向更高的分辨率层(higher resolution layers)传播。结果是，扩张路径基本对称于收缩路径。网络不存在任何全连接层(fully connected layers)，并且，只使用每个卷积的有效部分，例如，分割图(segmentation map)只包含这样一些像素点，这些像素点的完整上下文都出现在输入图像中。为了预测图像边界区域的像素点，我们采用镜像图像的方式补全缺失的环境像素。这个tiling方法在使用网络分割大图像时是非常有用的，因为如果不这么做，GPU显存会限制图像分辨率。
我们的训练数据太少，因此我们采用弹性形变的方式增加数据。这可以让模型学习得到形变不变性。这对医学图像分割是非常重要的，因为组织的形变是非常常见的情况，并且计算机可以很有效的模拟真实的形变。在[3]中指出了在无监督特征学习中，增加数据以获取不变性的重要性。

参考资料

DeepLab 系列

  • [ ] TODO

参考资料

边框回顾（Bounding-Box Regression）

如下图所示，绿色的框表示真实值Ground Truth, 红色的框为Selective Search提取的候选区域/框Region Proposal。那么即便红色的框被分类器识别为飞机，但是由于红色的框定位不准(IoU<0.5)， 这张图也相当于没有正确的检测出飞机。

如果我们能对红色的框进行微调fine-tuning，使得经过微调后的窗口跟Ground Truth 更接近， 这样岂不是定位会更准确。 而Bounding-box regression 就是用来微调这个窗口的。

边框回归是什么？

对于窗口一般使用四维向量(x,y,w,h)(x,y,w,h) 来表示， 分别表示窗口的中心点坐标和宽高。 对于图2, 红色的框 P 代表原始的Proposal, 绿色的框 G 代表目标的 Ground Truth， 我们的目标是寻找一种关系使得输入原始的窗口 P 经过映射得到一个跟真实窗口 G 更接近的回归窗口G^。

所以，边框回归的目的即是：给定(Px,Py,Pw,Ph)寻找一种映射f， 使得f(Px,Py,Pw,Ph)=(Gx^,Gy^,Gw^,Gh^)并且(Gx^,Gy^,Gw^,Gh^)≈(Gx,Gy,Gw,Gh)

边框回归怎么做的？

那么经过何种变换才能从图2中的窗口 P 变为窗口G^呢？ 比较简单的思路就是: 平移+尺度放缩

先做平移(Δx,Δy)，Δx=Pwdx(P),Δy=Phdy(P)这是R-CNN论文的：
G^x=Pwdx(P)+Px,(1)
G^y=Phdy(P)+Py,(2)

然后再做尺度缩放(Sw,Sh), Sw=exp(dw(P)),Sh=exp(dh(P)),对应论文中：
G^w=Pwexp(dw(P)),(3)
G^h=Phexp(dh(P)),(4)

观察(1)-(4)我们发现， 边框回归学习就是dx(P),dy(P),dw(P),dh(P)这四个变换。

下一步就是设计算法那得到这四个映射。

线性回归就是给定输入的特征向量 X, 学习一组参数 W, 使得经过线性回归后的值跟真实值 Y(Ground Truth)非常接近. 即Y≈WX。 那么 Bounding-box 中我们的输入以及输出分别是什么呢？

Input:
RegionProposal→P=(Px,Py,Pw,Ph)这个是什么？ 输入就是这四个数值吗？其实真正的输入是这个窗口对应的 CNN 特征，也就是 R-CNN 中的 Pool5 feature（特征向量）。 (注：训练阶段输入还包括 Ground Truth， 也就是下边提到的t∗=(tx,ty,tw,th))

Output:
需要进行的平移变换和尺度缩放 dx(P),dy(P),dw(P),dh(P)，或者说是Δx,Δy,Sw,Sh。我们的最终输出不应该是 Ground Truth 吗？ 是的， 但是有了这四个变换我们就可以直接得到 Ground Truth。

这里还有个问题， 根据(1)~(4)我们可以知道， P 经过 dx(P),dy(P),dw(P),dh(P)得到的并不是真实值 G，而是预测值G^。的确，这四个值应该是经过 Ground Truth 和 Proposal 计算得到的真正需要的平移量(tx,ty)和尺度缩放(tw,th)。

这也就是 R-CNN 中的(6)~(9)：
tx=(Gx−Px)/Pw,(6)

ty=(Gy−Py)/Ph,(7)

tw=log(Gw/Pw),(8)

th=log(Gh/Ph),(9)

那么目标函数可以表示为 d∗(P)=wT∗Φ5(P)，Φ5(P)是输入 Proposal 的特征向量，w∗是要学习的参数（*表示 x,y,w,h， 也就是每一个变换对应一个目标函数） , d∗(P) 是得到的预测值。

我们要让预测值跟真实值t∗=(tx,ty,tw,th)差距最小， 得到损失函数为：
Loss=∑iN(ti∗−w^T∗ϕ5(Pi))2

函数优化目标为：

W∗=argminw∗∑iN(ti∗−w^T∗ϕ5(Pi))2+λ||w^∗||2

利用梯度下降法或者最小二乘法就可以得到 w∗。

参考资料

Xception

  • [ ] TODO

SENet

SENet

论文：《Squeeze-and-Excitation Networks》

论文链接：https://arxiv.org/abs/1709.01507

代码地址：https://github.com/hujie-frank/SENet

论文的动机是从特征通道之间的关系入手，希望显式地建模特征通道之间的相互依赖关系。另外，没有引入一个新的空间维度来进行特征通道间的融合，而是采用了一种全新的“特征重标定”策略。具体来说，就是通过学习的方式来自动获取到每个特征通道的重要程度，然后依照这个重要程度去增强有用的特征并抑制对当前任务用处不大的特征，通俗来讲，就是让网络利用全局信息有选择的增强有益feature通道并抑制无用feature通道，从而能实现feature通道自适应校准。

Schema of SE-Inception and SE-ResNet modules

参考资料

SKNet

  • [ ] TODO

参考资料

GCNet

  • [ ] TODO

参考资料

Octave Convolution

  • [ ] TODO

参考资料

MobileNet 系列（V1-V3）

  • [ ] TODO

MobileNetV1

参考资料

MobileNetV2

  • [ ] TODO

MobileNetV3

MobileNet系列为什么快？各有多少层？多少参数？

  • [ ] TODO

MobileNetV1、MobileNetV2和MobileNetV3有什么区别

MobileNetv1：在depthwise separable convolutions（参考Xception）方法的基础上提供了高校模型设计的两个选择：宽度因子（width multiplie）和分辨率因子（resolution multiplier）。深度可分离卷积depthwise separable convolutions（参考Xception）的本质是冗余信息更小的稀疏化表达。

下面介绍两幅Xception中 depthwise separable convolution的图示：

image.png

image.png

深度可分离卷积的过程是①用16个3×3大小的卷积核（1通道）分别与输入的16通道的数据做卷积（这里使用了16个1通道的卷积核，输入数据的每个通道用1个3×3的卷积核卷积），得到了16个通道的特征图，我们说该步操作是depthwise（逐层）的，在叠加16个特征图之前，②接着用32个1×1大小的卷积核（16通道）在这16个特征图进行卷积运算，将16个通道的信息进行融合（用1×1的卷积进行不同通道间的信息融合），我们说该步操作是pointwise（逐像素）的。这样我们可以算出整个过程使用了3×3×16+（1×1×16）×32 =656个参数。

注：上述描述与标准的卷积非常的不同，第一点在于使用非1x1卷积核时，是单channel的（可以说是1通道），即上一层输出的每个channel都有与之对应的卷积核。而标准的卷积过程，卷积核是多channel的。第二点在于使用1x1卷积核实现多channel的融合，并利用多个1x1卷积核生成多channel。表达的可能不是很清楚，但结合图示其实就容易明白了。

一般卷积核的channel也常称为深度（depth），所以叫做深度可分离，即原来为多channel组合，现在变成了单channel分离。

参考资料

MobileNetv2为什么会加shotcut？

  • [ ] TODO

MobileNet V2中的Residual结构最先是哪个网络提出来的？

  • [ ] TODO

ShuffleNet 系列（V1-V2++）

  • [ ] TODO

ShuffleNetV1

ShuffleNetV2

  • [ ] TODO

参考资料

IGC 系列（V1-V3）

  • [ ] TODO

参考资料

深度可分离网络（Depth separable convolution）

  • [ ] TODO

计算机视觉

IoU

IoU（Intersection over Union），又称重叠度/交并比。

1 NMS：当在图像中预测多个proposals、pred bboxes时，由于预测的结果间可能存在高冗余（即同一个目标可能被预测多个矩形框），因此可以过滤掉一些彼此间高重合度的结果；具体操作就是根据各个bbox的score降序排序，剔除与高score bbox有较高重合度的低score bbox，那么重合度的度量指标就是IoU；

2 mAP：得到检测算法的预测结果后，需要对pred bbox与gt bbox一起评估检测算法的性能，涉及到的评估指标为mAP，那么当一个pred bbox与gt bbox的重合度较高（如IoU score > 0.5），且分类结果也正确时，就可以认为是该pred bbox预测正确，这里也同样涉及到IoU的概念；

提到IoU，大家都知道怎么回事，讲起来也都头头是道，我拿两个图示意下（以下两张图都不是本人绘制）：

img

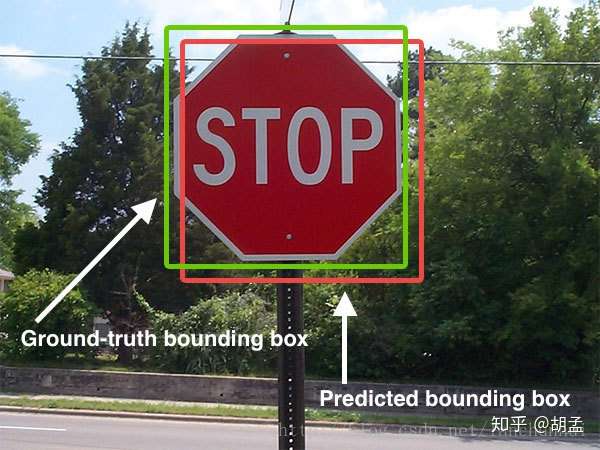
绿框：gt bbox；

红框：pred bbox；

那么IoU的计算如下：

img

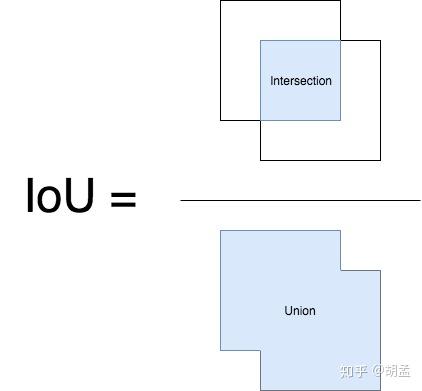
简单点说，就是gt bbox、pred bbox交集的面积 / 二者并集的面积；

好了，现在理解IoU的原理和计算方法了，就应该思考如何函数实现了，这也是我写本笔记的原因；

有次面试实习生的时候，一位同学讲各类目标检测算法头头是道，说到自己复现某某算法的mAP高达多少多少，问完他做的各种改进后，觉得小伙子还是挺不错的；

后来我是想着问问mAP的概念吧，但又觉得有点太复杂，不容易一下讲清楚细节，那就问问IoU吧，结果那位小朋友像傻逼一样看着我，说就是两个bbox的交并比啊，我说那要不你写段伪代码实现下吧，既然简单的话，应该实现起来还是很快的（一般我们也都会有这么个写伪代码的面试步骤，考考动手能力和思考能力吧）；然后那位自信满满的小伙子就立马下手开始写了，一般听完题目直接写代码的面试者，有两种可能性：

1 确实写过类似的代码，已经知道里面有哪些坑了，直接信手拈来；

2 没写过类似的代码，且把问题考虑简单化了；

我说你不用着急写，可以先想想两个bbox出现交集的各种情况，如两个bbox如何摆放，位置，以及二者不存在交集的情况等等（看到IoU的具体代码后，你会发现虽然只有寥寥几行代码，但其实已经处理好此类情况了），然后他画了几个图，瞬间表情严肃起来，然后我继续说你还得考虑一个bbox包围另一个bbox；两bbox并不是边角相交，而是两条边相交的特殊情况等等（说到这里我觉得自己也坏坏滴，故意把人家往歪路上牵。。。但主要是看得出来他确实不熟悉IoU的实现了），他就又画了若干种情况，最后开始写代码，刚开始还ok，写了十几行，后来越加越多，草稿纸上也涂涂改改越来越夸张，脸也越胀越红；我看了下他的代码，觉得他思路还行，考虑的还挺周全的，就给了他一个提示：你有没有考虑到你列举的这些情况，有一些可以合并的？他看了下，觉得是可以合并一些情况，就删减了部分代码，稿纸上就更乱了，然后又问他：可不可以继续合并；他就又继续思考了。。。大概是后来越想越复杂，就给我说这个原理他懂的，代码也看过，但现在确实是没能写出来；然后我安慰他，说如果没写过的话，确实是会把问题考虑简单化 / 复杂化，不过我并不是专门考个题目刁难你，而是因为你一直都在做目标检测，所以以为IoU的原理、实现你应该会比较熟悉的，写起代码也应该没问题的；而且你的思路也挺好的，先考虑各种复杂情况，再慢慢合并一些情况，先从1到N，再回到1就行，只不过可能到了N，没考虑到如何再回到1了；

再后来，也面试过其他实习生同学，问到了IoU的实现，很可惜，好像还没有一位同学能圆满写出来的。。。当然了，可能是我有时候过于抠细节了，不利于他们的发挥吧。。。

好了，以上都是废话，看看如何实现吧；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
# -*- coding: utf-8 -*-
#
# This is the python code for calculating bbox IoU,
# By running the script, we can get the IoU score between pred / gt bboxes
#
# Author: hzhumeng01 2018-10-19
# copyright @ netease, AI group

from __future__ import print_function, absolute_import
import numpy as np

def get_IoU(pred_bbox, gt_bbox):
    """
    return iou score between pred / gt bboxes
    :param pred_bbox: predict bbox coordinate
    :param gt_bbox: ground truth bbox coordinate
    :return: iou score
    """

    # bbox should be valid, actually we should add more judgements, just ignore here...
    # assert ((abs(pred_bbox[2] - pred_bbox[0]) > 0) and
    #         (abs(pred_bbox[3] - pred_bbox[1]) > 0))
    # assert ((abs(gt_bbox[2] - gt_bbox[0]) > 0) and
    #         (abs(gt_bbox[3] - gt_bbox[1]) > 0))

    # -----0---- get coordinates of inters
    ixmin = max(pred_bbox[0], gt_bbox[0])
    iymin = max(pred_bbox[1], gt_bbox[1])
    ixmax = min(pred_bbox[2], gt_bbox[2])
    iymax = min(pred_bbox[3], gt_bbox[3])
    iw = np.maximum(ixmax - ixmin + 1., 0.)
    ih = np.maximum(iymax - iymin + 1., 0.)

    # -----1----- intersection
    inters = iw * ih

    # -----2----- union, uni = S1 + S2 - inters
    uni = ((pred_bbox[2] - pred_bbox[0] + 1.) * (pred_bbox[3] - pred_bbox[1] + 1.) +
           (gt_bbox[2] - gt_bbox[0] + 1.) * (gt_bbox[3] - gt_bbox[1] + 1.) -
           inters)

    # -----3----- iou
    overlaps = inters / uni

    return overlaps


def get_max_IoU(pred_bboxes, gt_bbox):
    """
    given 1 gt bbox, >1 pred bboxes, return max iou score for the given gt bbox and pred_bboxes
    :param pred_bbox: predict bboxes coordinates, we need to find the max iou score with gt bbox for these pred bboxes
    :param gt_bbox: ground truth bbox coordinate
    :return: max iou score
    """

    # bbox should be valid, actually we should add more judgements, just ignore here...
    # assert ((abs(gt_bbox[2] - gt_bbox[0]) > 0) and
    #         (abs(gt_bbox[3] - gt_bbox[1]) > 0))

    if pred_bboxes.shape[0] > 0:
        # -----0---- get coordinates of inters, but with multiple predict bboxes
        ixmin = np.maximum(pred_bboxes[:, 0], gt_bbox[0])
        iymin = np.maximum(pred_bboxes[:, 1], gt_bbox[1])
        ixmax = np.minimum(pred_bboxes[:, 2], gt_bbox[2])
        iymax = np.minimum(pred_bboxes[:, 3], gt_bbox[3])
        iw = np.maximum(ixmax - ixmin + 1., 0.)
        ih = np.maximum(iymax - iymin + 1., 0.)

        # -----1----- intersection
        inters = iw * ih

        # -----2----- union, uni = S1 + S2 - inters
        uni = ((gt_bbox[2] - gt_bbox[0] + 1.) * (gt_bbox[3] - gt_bbox[1] + 1.) +
               (pred_bboxes[:, 2] - pred_bboxes[:, 0] + 1.) * (pred_bboxes[:, 3] - pred_bboxes[:, 1] + 1.) -
               inters)

        # -----3----- iou, get max score and max iou index
        overlaps = inters / uni
        ovmax = np.max(overlaps)
        jmax = np.argmax(overlaps)

    return overlaps, ovmax, jmax

if __name__ == "__main__":

    # test1
    pred_bbox = np.array([50, 50, 90, 100])   # top-left: <50, 50>, bottom-down: <90, 100>, <x-axis, y-axis>
    gt_bbox = np.array([70, 80, 120, 150])
    print (get_IoU(pred_bbox, gt_bbox))
    
    # test2
    pred_bboxes = np.array([[15, 18, 47, 60],
                          [50, 50, 90, 100],
                          [70, 80, 120, 145],
                          [130, 160, 250, 280],
                          [25.6, 66.1, 113.3, 147.8]])
    gt_bbox = np.array([70, 80, 120, 150])
    print (get_max_IoU(pred_bboxes, gt_bbox))

其实计算bbox间IoU唯一的难点就在计算intersection，代码的实现很简单：

1
2
3
4
5
6
7
ixmin = max(pred_bbox[0], gt_bbox[0])
iymin = max(pred_bbox[1], gt_bbox[1])
ixmax = min(pred_bbox[2], gt_bbox[2])
iymax = min(pred_bbox[3], gt_bbox[3])
iw = np.maximum(ixmax - ixmin + 1., 0.)
ih = np.maximum(iymax - iymin + 1., 0.)

比较厉害的就是，以上短短六行代码就可以囊括所有pred bbox与gt bbox间的关系，不管是bboxes间相交 / 不相交，各种相交形式等等；我们在画图分析两个bbox间的关系时，会考虑各种情况，动手实践时会发现很复杂，是因为我们陷入了一种先入为主的思维，就是pred bbox与gt bbox有一个先后顺序，即我们认定了pred bbox为画图中的第一个bbox，gt bbox为第二个，这样在二者有不同位置关系时，就得考虑各种坐标判断情况，但若此时交换二者位置，其实并不影响我们计算IoU；

以上六行代码也印证了这个观点，直接计算两个bbox的相交边框坐标即可，若不相交得到的结果中，必有ixmax < ixmin、iymax - iymin其一成立，此时iw、ih就为0了；

好了，以上就是IoU的计算，原理比较简单，具体分析比较复杂，实现却异常简单，但通过对问题的深入分析，也能加深我们对知识的理解；

代码我传到github上了，比较简单：IoU_demo.py

参考资料

如何计算 mIoU？

Mean Intersection over Union(MIoU，均交并比)，为语义分割的标准度量。其计算两个集合的交集和并集之比，在语义分割问题中，这两个集合为真实值（ground truth）和预测值（predicted segmentation）。这个比例可以变形为TP（交集）比上TP、FP、FN之和（并集）。在每个类上计算IoU，然后取平均。

pij表示真实值为i，被预测为j的数量。

直观理解

红色圆代表真实值，黄色圆代表预测值。橙色部分为两圆交集部分。

  • MPA（Mean Pixel Accuracy，均像素精度）：计算橙色与红色圆的比例；
  • MIoU：计算两圆交集（橙色部分）与两圆并集（红色+橙色+黄色）之间的比例，理想情况下两圆重合，比例为1。

Tensorflow源码解析

Tensorflow主要用tf.metrics.mean_iou来计算mIoU，下面解析源码：

第一步：计算混淆矩阵

混淆矩阵例子

img

Pytorch源码解

Pytorch基本计算思路和上面是一样的，代码很简洁，就不过多介绍了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class IOUMetric:
    """
    Class to calculate mean-iou using fast_hist method
    """

    def __init__(self, num_classes):
        self.num_classes = num_classes
        self.hist = np.zeros((num_classes, num_classes))

    def _fast_hist(self, label_pred, label_true):
        mask = (label_true >= 0) & (label_true < self.num_classes)
        hist = np.bincount(
            self.num_classes * label_true[mask].astype(int) +
            label_pred[mask], minlength=self.num_classes ** 2).reshape(self.num_classes, self.num_classes)
        return hist

    def add_batch(self, predictions, gts):
        for lp, lt in zip(predictions, gts):
            self.hist += self._fast_hist(lp.flatten(), lt.flatten())

    def evaluate(self):
        acc = np.diag(self.hist).sum() / self.hist.sum()
        acc_cls = np.diag(self.hist) / self.hist.sum(axis=1)
        acc_cls = np.nanmean(acc_cls)
        iu = np.diag(self.hist) / (self.hist.sum(axis=1) + self.hist.sum(axis=0) - np.diag(self.hist))
        mean_iu = np.nanmean(iu)
        freq = self.hist.sum(axis=1) / self.hist.sum()
        fwavacc = (freq[freq > 0] * iu[freq > 0]).sum()
        return acc, acc_cls, iu, mean_iu, fwavacc

Python 简版实现

1
2
3
4
5
6
7
8
9
10
11
#RT:RightTop
#LB:LeftBottom
def IOU(rectangle A, rectangleB):
    W = min(A.RT.x, B.RT.x) - max(A.LB.x, B.LB.x)
    H = min(A.RT.y, B.RT.y) - max(A.LB.y, B.LB.y)
    if W <= 0 or H <= 0:
        return 0;
    SA = (A.RT.x - A.LB.x) * (A.RT.y - A.LB.y)
    SB = (B.RT.x - B.LB.x) * (B.RT.y - B.LB.y)
    cross = W * H
    return cross/(SA + SB - cross)

参考资料

mAP

参考资料

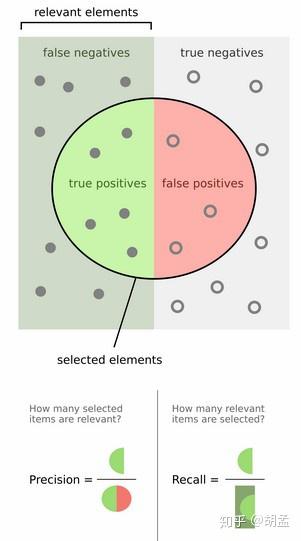
mAP定义及相关概念

  • mAP: mean Average Precision, 即各类别AP的平均值
  • AP: PR曲线下面积，后文会详细讲解
  • PR曲线: Precision-Recall曲线
  • Precision: TP / (TP + FP)
  • Recall: TP / (TP + FN)
  • TP: IoU>0.5的检测框数量（同一Ground Truth只计算一次）
  • FP: IoU<=0.5的检测框，或者是检测到同一个GT的多余检测框的数量
  • FN: 没有检测到的GT的数量

本笔记介绍目标检测的一个基本概念：AP、mAP（mean Average Precision），做目标检测的同学想必对这个词语耳熟能详了，不管是Pascal VOC，还是COCO，甚至是人脸检测的wider face数据集，都使用到了AP、mAP的评估方式，那么AP、mAP到底是什么？如何计算的？

如果希望一篇笔记讲明白目标检测中的mAP，感觉自己表达能力有限，可能搞不定，但如果希望一下能明白mAP含义的，可以参照引用链接；今天主要介绍下mAP的计算方式，假定前提为已经明白了precision、recall、tp、fp等概念，当然了，不明白也没关系，下一篇介绍Pascal VOC评估工具时会再详细介绍；

1 图像检索mAP

那么mAP到底是什么东西，如何计算？网上已经有了很多很多资料，但其实很多感觉都讲不清楚，我看到过一个在图像检索里面介绍得最好的示意图，我们先以图像检索中的mAP为例说明，其实目标检测中mAP与之几乎一样：

img

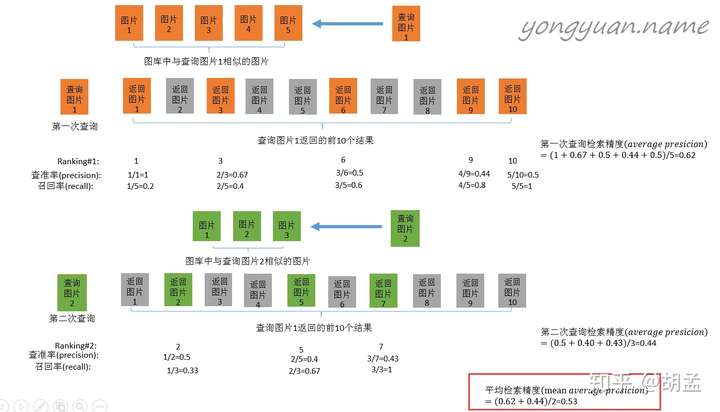
以上是图像检索中mAP的计算案例，简要说明下：

1 查询图片1在图像库中检索相似图像，假设图像库中有五张相似图像，表示为图片1、…、图片5，排名不分先后；

2 检索（过程略），返回了top-10图像，如上图第二行，橙色表示相似的图像，灰色为无关图像；

3 接下来就是precision、recall的计算过程了，结合上图比较容易理解；

以返回图片6的节点为例：

top-6中，有3张图像确实为相似图像，另三张图像为无关图像，因此precision = 3 / 6；同时，总共五张相似图像，top-6检索出来了三张，因此recall = 3 / 5；

4 然后计算AP，可以看右边的计算方式，可以发现是把列出来的查询率(precision)相加取平均，那么最关键的问题来了：为什么选择这几张图像的precision求平均？可惜图中并没有告诉我们原因；

但其实不难，一句话就是：选择每个recall区间内对应的最高precision；

举个栗子，以上图橙色检索案例为例，当我们只选择top-1作为检索结果返回（也即只返回一个检索结果）时，检索性能为：

1
2
3
4
5
6
7
8
9
10
top-1：recall = 1 / 5、precision = 1 / 1；# 以下类推；
top-2：recall = 1 / 5、precision = 1 / 2；
top-3：recall = 2 / 5、precision = 2 / 3；
top-4：recall = 2 / 5、precision = 2 / 4；
top-5：recall = 2 / 5、precision = 2 / 5；
top-6：recall = 3 / 5、precision = 3 / 6；
top-7：recall = 3 / 5、precision = 3 / 7；
top-8：recall = 3 / 5、precision = 3 / 8；
top-9：recall = 4 / 5、precision = 4 / 9；
top-10：recall = 5 / 5、precision = 5 / 10；

结合上面清单，先找找recall = 1 / 5区间下的最高precision，对应着precision = 1 / 1；

同理，recall = 2 / 5区间下的最高precision，对应着precision = 2 / 3；

recall = 3 / 5区间下的最高precision，对应着precision = 3 / 6；依次类推；

这样AP = (1 / 1 + 2 / 3 + 3 / 6 + 4 / 9 + 5 / 10) / 5；

那么mAP是啥？计算所有检索图像返回的AP均值，对应上图就是橙、绿突图像计算AP求均值，对应红色框；

这样mAP就计算完毕啦~~~是不是很容易理解？目标检测的mAP也是类似操作了；

2 目标检测中mAP计算流程

这里面我引用的是一篇博文，以下内容大多参考该博文，做了一些小修改；

下面的例子也很容易理解，假设检测人脸吧，gt label表示1为人脸，0为bg，某张图像中共检出了20个pred bbox，id：1 ~ 20，并对应了confidence score，gt label也很容易获得，pred bbox与gt bbox算IoU，给定一个threshold，那么就知道该pred bbox是否为正确的预测结果了，就对应了其gt label；—— 其实下表不应该这么理解的，但我们还是先这么认为，忽略差异吧，先直捣黄龙，table 1：

img

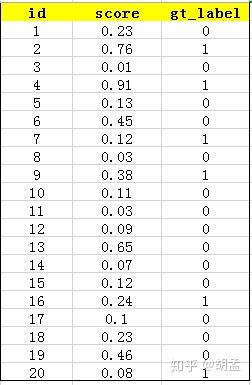
接下来对confidence score排序，得到table 2：

img

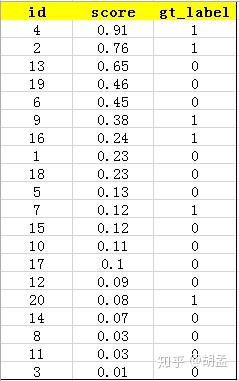
这张表很重要，接下来的precision和recall都是依照这个表计算的，那么这里的confidence score其实就和图像检索中的相似度关联上了，具体地，就是如第一节的图像检索中，虽然我们计算mAP没在乎其检索返回的先后顺序，但top1肯定是与待检索图像最相似的，对应的similarity score最高，对人脸检测而言，pred bbox的confidence score最高，也说明该bbox最有可能是人脸；

然后计算precision和recall，这两个标准的定义如下：

img

上面的图看看就行，能理解就理解，不理解可以参照第一节图像检索的例子来理解；

现以返回的top-5结果为例，如table 3：

img

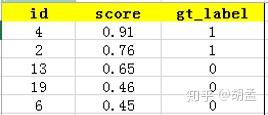
在这个例子中，true positives就是指id = 4、2的pred bbox，false positives就是指id = 13、19、6的pred bbox。方框内圆圈外的元素（false negatives + true negatives）是相对于方框内的元素而言，在这个例子中，是指confidence score排在top-5之外的元素，即table 4：

img

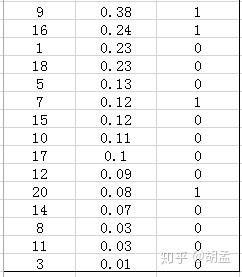
其中，false negatives是指id = 9、16、7、20的4个pred bbox，true negatives是指id = 1、18、5、15、10、17、12、14、8、11、3的11个pred bbox；

那么，这个例子中Precision = 2 / 5 = 40%，意思是对于人脸检测而言，我们选定了5 pred bbox，其中正确的有2个，即准确率为40%；Recall = 2 / 6 = 33%，意思是该图像中共有6个人脸，但是因为我们只召回了2个，所以召回率为33%；

实际的目标检测任务中，我们通常不满足只通过top-5来衡量一个模型的好坏，而是需要知道从top-1到top-N（N是所有pred bbox，本文中为20）对应的precision和recall；显然随着我们选定的pred bbox越来也多，recall一定会越来越高，而precision整体上会呈下降趋势；把recall当成横坐标，precision当成纵坐标，即可得到常用的precision-recall曲线，以上例子的precision-recall曲线如fig 1：

img

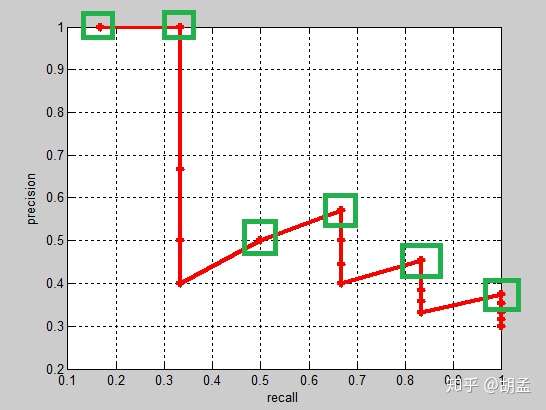
以上图像如何计算的？可以参照第一节图像检索中的栗子，还是比较容易理解的吧；

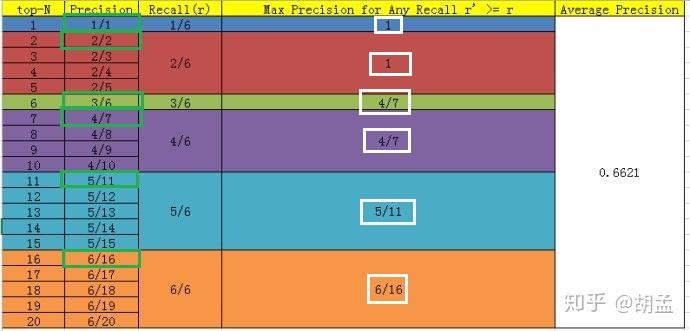
上面的每个红点，就相当于根据table 2，按照第一节中图像检索的方式计算出来的，也可以直接参照下面的table 5，自己心里算一算；

那么按照选择每个recall区间内对应的最高precision的计算方案，各个recall区间内对应的top-precision，就刚好如fig 1中的绿色框位置，可以进一步结合table 5中的绿色框理解；

好了，那么对这张图像而言，其AP = （1 / 1 + 2 / 2 + 3 / 6 + 4 / 7 + 5 / 11 + 6 / 16）/ 6；这是针对单张图像而言，所有图像也类似方式计算，那么就可以根据所有图像上的pred bbox，采用同样的方式，就计算出了所有图像上人脸这个类的AP；因为人脸检测只有一个类，如Pascal VOC这种20类的，每类都可以计算出一个AP，那么AP_total / 20，就是mAP啦；

但是等等，有没有发现table 5中，计算方式好像跟我们讲的有一点不一样？我们继续看看；

3 Pascal VOC的两套mAP评估标准

Pascal VOC中对mAP的计算经历了两次迭代，一种是VOC07的计算标准，对应绿色框：

首先设定一组阈值，T = [0、0.1、0.2、…、1]，然后对于recall大于每一个阈值Ti（比如recall > 0.3），我们都会在该recall区间内得到一个对应的最大precision，这样我们就计算出了11个precision；——- 这里与上两节介绍的概念是一样的，只不过上面recall的区间是参照gt label来划分的，这里是我们人为划分的11个节点；

AP即为这11个precision的平均值，这种方法英文叫做11-point interpolated average precision；有了一个类的AP，所有类的AP均值即为mAP；

另一种是VOC10的计算标准，对应白色框：

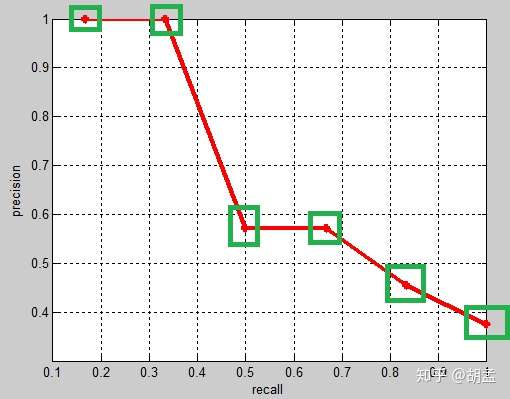
新的计算方法假设N个pred bbox中有M个gt bbox，那么我们会得到M个recall节点（1 / M、2 / M、…、 M / M），对于每个recall值 r，我们可以计算出对应（r’ > r）的最大precision，然后对这M个precision值取平均即得到最后的AP值，计算方法如table 5：

img

从VOC07的绿框、VOC10的白框对比可知，差异主要在recall = 3 / 6下的precision，可以发现VOC07找的top-precision是在该recall区间段内的，但VOC10相当于是向后查找的，需确保该recall阈值以后的区间内，对应的是top-precision，可知4 / 7 > 3 / 6，因此使用4 / 7替换了3 / 6，其他recall阈值下的操作方式类似；

那么代码的实操中，就得从按照recall阈值从后往前计算了，这样就可以一遍就梭哈出所有结果，如果按recall从前往后计算，就有很多重复性计算（不断地重复向后recall区间内查找top-precision），然后呢，就可以使用到动态规划的方式做了，理论结合实践啊有木有~~~

那么VOC10下，相应的Precision-Recall曲线如fig 2，可以发现这条曲线是单调递减的，剩下的AP计算方式就与VOC07相同了：

这里还需要继续一点，VOC07是11点插值的AP方式，等于是卡了11个离散的点，划分10个区间来计算AP，但VOC10是是根据recall值变化的区间来计算的，在这个栗子里，recall只变化了6次，但如果recall变化很多次，如100次、1000次、9999次等，就可以认为是一种 “伪” 连续的方式计算了；

img

总结：

AP衡量的是模型在每个类别上的好坏，mAP衡量的是模型在所有类别上的好坏，得到AP后mAP的计算就变得很简单了，就是取所有类别AP的平均值。

3 代码

直接上代码吧，这个函数假设我们已经得到了排序好的precision、recall的list，对应上图fig 2，进一步可以参照第一节中的清单理解；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# VOC-style mAP，分为两个计算方式，之所有两个计算方式，是因为2010年后VOC更新了评估方法，因此就有了07-metric和else...
def voc_ap(rec, prec, use_07_metric=False):
    """
    average precision calculations
    [precision integrated to recall]
    :param rec: recall list
    :param prec: precision list
    :param use_07_metric: 2007 metric is 11-recall-point based AP
    :return: average precision
    """
    if use_07_metric:
        # 11 point metric
        ap = 0.
        # VOC07是11点插值的AP方式，等于是卡了11个离散的点，划分10个区间来计算AP
        for t in np.arange(0., 1.1, 0.1):
            if np.sum(rec >= t) == 0:
                p = 0    # recall卡的阈值到顶了，1.1
            else:
                p = np.max(prec[rec >= t])   # VOC07：选择每个recall区间内对应的最高precision的计算方案
            ap = ap + p / 11.    # 11-recall-point based AP
    else:
        # correct AP calculation
        # first append sentinel values at the end
        mrec = np.concatenate(([0.], rec, [1.]))
        mpre = np.concatenate(([0.], prec, [0.]))

        # compute the precision envelope
        for i in range(mpre.size - 1, 0, -1):
            mpre[i - 1] = np.maximum(mpre[i - 1], mpre[i])    # 这个是不是动态规划？从后往前找之前区间内的top-precision，多么优雅的代码呀~~~

        # to calculate area under PR curve, look for points where X axis (recall) changes value
        # 上面的英文，可以结合着fig 2的绿框理解，一目了然
        # VOC10是是根据recall值变化的区间来计算的，如果recall变化很多次，就可以认为是一种 “伪” 连续的方式计算了，以下求的是recall的变化
        i = np.where(mrec[1:] != mrec[:-1])[0]

        # 计算AP，这个计算方式有点玄乎，是一个积分公式的简化，应该是对应的fig 2中红色曲线以下的面积，之前公式的推导我有看过，现在有点忘了，麻烦各位同学补充一下
        # 现在理解了，不难，公式：sum (\Delta recall) * prec，其实结合fig2和下面的图，不就是算的积分么？如果recall划分得足够细，就可以当做连续数据，然后以下公式就是积分公式，算的precision、recall下面的面积了
        ap = np.sum((mrec[i + 1] - mrec[i]) * mpre[i + 1])
    return ap

通常VOC10标准下计算的mAP值会高于VOC07，原因如下，我就不详细介绍了：

Interpolated average precision
Some authors choose an alternate approximation that is called the interpolated average precision. Often, they still call it average precision. Instead of using P(k), the precision at a retrieval cutoff of k images, the interpolated average precision uses:

img

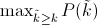
In other words, instead of using the precision that was actually observed at cutoff k, the interpolated average precision uses the maximum precision observed across all cutoffs with higher recall. The full equation for computing the interpolated average precision is:

img

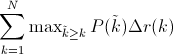
Visually, here’s how the interpolated average precision compares to the approximated average precision (to show a more interesting plot, this one isn’t from the earlier example):

img

The approximated average precision closely hugs the actually observed curve. The interpolated average precision over estimates the precision at many points and produces a higher average precision value than the approximated average precision.

Further, there are variations on where to take the samples when computing the interpolated average precision. Some take samples at a fixed 11 points from 0 to 1: {0, 0.1, 0.2, …, 0.9, 1.0}. This is called the 11-point interpolated average precision. Others sample at every k where the recall changes.

参考资料

如何计算 mAP？

每类的AP/类别数

参考资料

目标检测度量标准

  • mAP

  • FPS

  • [ ] TODO

参考资料

图像分割度量标准

  • [ ] TODO
  • PA
  • MP
  • mIoU
  • FWIoU
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class IOUMetric:
    """
    Class to calculate mean-iou using fast_hist method
    """

    def __init__(self, num_classes):
        self.num_classes = num_classes
        self.hist = np.zeros((num_classes, num_classes))

    def _fast_hist(self, label_pred, label_true):
        mask = (label_true >= 0) & (label_true < self.num_classes)
        hist = np.bincount(
            self.num_classes * label_true[mask].astype(int) +
            label_pred[mask], minlength=self.num_classes ** 2).reshape(self.num_classes, self.num_classes)
        return hist

    def add_batch(self, predictions, gts):
        for lp, lt in zip(predictions, gts):
            self.hist += self._fast_hist(lp.flatten(), lt.flatten())

    def evaluate(self):
        acc = np.diag(self.hist).sum() / self.hist.sum()
        acc_cls = np.diag(self.hist) / self.hist.sum(axis=1)
        acc_cls = np.nanmean(acc_cls)
        iu = np.diag(self.hist) / (self.hist.sum(axis=1) + self.hist.sum(axis=0) - np.diag(self.hist))
        mean_iu = np.nanmean(iu)
        freq = self.hist.sum(axis=1) / self.hist.sum()
        fwavacc = (freq[freq > 0] * iu[freq > 0]).sum()
        return acc, acc_cls, iu, mean_iu, fwavacc

参考资料

非极大值抑制NMS

NMS的作用是将重复的检测框去掉

pytorch IoU代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# IOU计算
    # 假设box1维度为[N,4]   box2维度为[M,4]
    def iou(self, box1, box2):
        N = box1.size(0)
        M = box2.size(0)

        lt = torch.max(  # 左上角的点
            box1[:, :2].unsqueeze(1).expand(N, M, 2),   # [N,2]->[N,1,2]->[N,M,2]
            box2[:, :2].unsqueeze(0).expand(N, M, 2),   # [M,2]->[1,M,2]->[N,M,2]
        )

        rb = torch.min(
            box1[:, 2:].unsqueeze(1).expand(N, M, 2),
            box2[:, 2:].unsqueeze(0).expand(N, M, 2),
        )

        wh = rb - lt  # [N,M,2]
        wh[wh < 0] = 0   # 两个box没有重叠区域
        inter = wh[:,:,0] * wh[:,:,1]   # [N,M]

        area1 = (box1[:,2]-box1[:,0]) * (box1[:,3]-box1[:,1])  # (N,)
        area2 = (box2[:,2]-box2[:,0]) * (box2[:,3]-box2[:,1])  # (M,)
        area1 = area1.unsqueeze(1).expand(N,M)  # (N,M)
        area2 = area2.unsqueeze(0).expand(N,M)  # (N,M)

        iou = inter / (area1+area2-inter)
        return iou

NMS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# NMS算法
    # bboxes维度为[N,4]，scores维度为[N,], 均为tensor
    def nms(self, bboxes, scores, threshold=0.5):
        x1 = bboxes[:,0]
        y1 = bboxes[:,1]
        x2 = bboxes[:,2]
        y2 = bboxes[:,3]
        areas = (x2-x1)*(y2-y1)   # [N,] 每个bbox的面积
        _, order = scores.sort(0, descending=True)    # 降序排列 这里返回的是indices

        keep = []
        while order.numel() > 0:       # torch.numel()返回张量元素个数
            if order.numel() == 1:     # 保留框只剩一个
                i = order.item()
                keep.append(i)
                break
            else:
                i = order[0].item()    # 保留scores最大的那个框box[i]
                keep.append(i)

            # 计算box[i]与其余各框的IOU(思路很好)
            xx1 = x1[order[1:]].clamp(min=x1[i])   # [N-1,]
            yy1 = y1[order[1:]].clamp(min=y1[i])
            xx2 = x2[order[1:]].clamp(max=x2[i])
            yy2 = y2[order[1:]].clamp(max=y2[i])
            inter = (xx2-xx1).clamp(min=0) * (yy2-yy1).clamp(min=0)   # [N-1,]

            iou = inter / (areas[i]+areas[order[1:]]-inter)  # [N-1,]
            idx = (iou <= threshold).nonzero().squeeze() # 注意此时idx为[N-1,] 而order为[N,]
            if idx.numel() == 0:
                break
            order = order[idx+1]  # 修补索引之间的差值
        return torch.LongTensor(keep)   # Pytorch的索引值为LongTensor

目标检测中的Anchor

anchor技术将问题转换为“这个固定参考框中有没有认识的目标，目标框偏离参考框多远”，不再需要多尺度遍历滑窗

参考资料

原始图片中的ROI如何映射到到feature map?

  • [ ] TODO

参考资料

请问Faster R-CNN和SSD 中为什么用smooth l1 loss，和l2有什么区别？

  1. 当预测框与 ground truth 差别过大时，梯度值不至于过大；
  2. 当预测框与 ground truth 差别很小时，梯度值足够小。

参考资料

给定5个人脸关键点和5个对齐后的点，求怎么变换的？

  • [ ] TODO

Bounding boxes 回归原理/公式

  • [ ] TODO

U-Net 和 FCN的区别

  • [ ] TODO

介绍KCF算法

  • [ ] TODO

介绍MobileNet-SSD算法

  • [ ] TODO

目标检测中的多尺度训练/测试？

  • [ ] TODO

多尺度训练对全卷积网络有效，一般设置几种不同尺度的图片，训练时每隔一定iterations随机选取一种尺度训练。这样训练出来的模型鲁棒性强，其可以接受任意大小的图片作为输入，使用尺度小的图片测试速度会快些，但准确度低，用尺度大的图片测试速度慢，但是准确度高。

参考资料

目标检测中的正负样本不平衡问题

参考资料

目标检测中的类别漏检问题该怎么解决？

  • [ ] TODO

参考资料

RPN

RPN 的损失函数

  • [ ] TODO

RPN中的anchor box是怎么选取的？

  • [ ] TODO

RoI Pooling

  • [ ] TODO

参考资料

RoI Align

  • [ ] TODO

参考资料

为什么深度学习中的图像分割要先编码再解码？

  • [ ] TODO

参考资料

NMS

本笔记介绍目标检测的另一个基本概念：NMS（non-maximum suppression），做目标检测的同学想必对这个词语耳熟能详了；

在检测图像中的目标时，不可避免地会检出很多bboxes + cls scores，这些bbox之间有很多是冗余的，一个目标可能会被多个bboxes检出，如果所有bboxes都输出，就很影响体验和美观了（同一个目标输出100个bboxes，想想都后怕~~~），一种方案就是提升cls scores的阈值，减少bbox数量的输出；另一种方案就是使用NMS，将同一目标内的bboxes按照cls score + IoU阈值做筛选，剔除冗余地、低置信度的bbox；

可能又会问了：为什么目标检测时，会有这么多无效、冗余检测框呢？这个。。。我的理解，是因为图像中没有目标尺度、位置的先验知识，为保证对目标的高召回，就必须使用滑窗、anchor / default bbox密集采样的方式，尽管检测模型能对每个anchor / default bbox做出 cls + reg，可以一定程度上剔除误检，但没有结合检出bbox的cls score + IoU阈值做筛选，而NMS就可以做到这一点；

1 NMS操作流程

NMS用于剔除图像中检出的冗余bbox，标准NMS的具体做法为：

step-1：将所有检出的output_bbox按cls score划分（如pascal voc分20个类，也即将output_bbox按照其对应的cls score划分为21个集合，1个bg类，只不过bg类就没必要做NMS而已）；

step-2：在每个集合内根据各个bbox的cls score做降序排列，得到一个降序的list_k；

step-3：从list_k中top1 cls score开始，计算该bbox_x与list中其他bbox_y的IoU，若IoU大于阈值T，则剔除该bbox_y，最终保留bbox_x，从list_k中取出；

step-4：选择list_k中top2 cls score(步骤3取出top 1 bbox_x后，原list_k中的top 2就相当于现list_k中的top 1了，但如果step-3中剔除的bbox_y刚好是原list_k中的top 2，就依次找top 3即可，理解这么个意思就行)，重复step-3中的迭代操作，直至list_k中所有bbox都完成筛选；

step-5：对每个集合的list_k，重复step-3、4中的迭代操作，直至所有list_k都完成筛选；

以上操作写的有点绕，不过如果理解NMS操作流程的话，再结合下图，应该还是非常好理解的；

img

2 代码学习

2.1 test_RFB.py

我选择了RFBNet里的代码介绍NMS，因为里面的流程基本上就是按照我说的操作进行了；

先看看test_RFB.py中的片段，通过以下代码可以发现，其对应着step-1、step5操作，就是说NMS操作是逐类进行的，图像中检出的所有bboxes，按照 cls 做划分，再每个类的bbox进一步做NMS；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
out = net(x)      # forward pass，这里相当于将图像 x 输入RFBNet，得到了pred cls + reg
boxes, scores = detector.forward(out,priors) # 结合priors，将pred reg（也即预测的offsets）解码成最终的pred bbox，如果理解anchor / default bbox操作流程，这个应该很好理解的；
boxes = boxes[0]
scores=scores[0]

# scale each detection back up to the image
boxes *= scale   # （0，1）区间坐标的bbox做尺度反正则化
boxes = boxes.cpu().numpy()
scores = scores.cpu().numpy()

for j in range(1, num_classes):      # 对每个类 j 的pred bbox单独做NMS，为什么index从1开始？因为0是bg，做NMS无意义
    inds = np.where(scores[:, j] > thresh)[0]     # 找到该类 j 下，所有cls score大于thresh的bbox，为什么选择大于thresh的bbox？因为score小于阈值的bbox，直接可以过滤掉，无需劳烦NMS
    if len(inds) == 0:    # 没有满足条件的bbox，返回空，跳过；
        all_boxes[j][i] = np.empty([0, 5], dtype=np.float32)
        continue
    c_bboxes = boxes[inds]
    c_scores = scores[inds, j]   # 找到对应类 j 下的score即可
    c_dets = np.hstack((c_bboxes, c_scores[:, np.newaxis])).astype(
        np.float32, copy=False)   # 将满足条件的bbox + cls score的bbox通过hstack完成合体

    keep = nms(c_dets, 0.45, force_cpu=args.cpu)    # NMS，返回需保存的bbox index：keep
    c_dets = c_dets[keep, :]
    all_boxes[j][i] = c_dets     # i 对应每张图像，j 对应图像中类别 j 的bbox清单

介绍以上代码处理流程，两个目的：

1 test_RFB.py的处理流程非常清晰，也很方便我们的理解；

2 for j in range(1, num_classes)操作表明了，NMS是逐类进行的，也即参与NMS的bbox都属于同一类；

2.2 py_cpu_nms.py

代码同样来自于FRBNet，结合注释可以发现引自Fast R-CNN；

这个代码是最简版的nms，跟第一节中NMS处理流程一致，非常适合学习，可以作为baseline，我加了个简单的main函数做测试；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
# --------------------------------------------------------
# Fast R-CNN
# Copyright (c) 2015 Microsoft
# Licensed under The MIT License [see LICENSE for details]
# Written by Ross Girshick
# --------------------------------------------------------

import numpy as np

def py_cpu_nms(dets, thresh):
    """Pure Python NMS baseline."""
    x1 = dets[:, 0]                     # pred bbox top_x
    y1 = dets[:, 1]                     # pred bbox top_y
    x2 = dets[:, 2]                     # pred bbox bottom_x
    y2 = dets[:, 3]                     # pred bbox bottom_y
    scores = dets[:, 4]              # pred bbox cls score

    areas = (x2 - x1 + 1) * (y2 - y1 + 1)    # pred bbox areas
    order = scores.argsort()[::-1]              # 对pred bbox按score做降序排序，对应step-2

    keep = []    # NMS后，保留的pred bbox
    while order.size > 0:
        i = order[0]          # top-1 score bbox
        keep.append(i)   # top-1 score的话，自然就保留了
        xx1 = np.maximum(x1[i], x1[order[1:]])   # top-1 bbox（score最大）与order中剩余bbox计算NMS
        yy1 = np.maximum(y1[i], y1[order[1:]])
        xx2 = np.minimum(x2[i], x2[order[1:]])
        yy2 = np.minimum(y2[i], y2[order[1:]])

        w = np.maximum(0.0, xx2 - xx1 + 1)
        h = np.maximum(0.0, yy2 - yy1 + 1)
        inter = w * h
        ovr = inter / (areas[i] + areas[order[1:]] - inter)      # 无处不在的IoU计算~~~

        inds = np.where(ovr <= thresh)[0]     # 这个操作可以对代码断点调试理解下，结合step-3，我们希望剔除所有与当前top-1 bbox IoU > thresh的冗余bbox，那么保留下来的bbox，自然就是ovr <= thresh的非冗余bbox，其inds保留下来，作进一步筛选
        order = order[inds + 1]   # 保留有效bbox，就是这轮NMS未被抑制掉的幸运儿，为什么 + 1？因为ind = 0就是这轮NMS的top-1，剩余有效bbox在IoU计算中与top-1做的计算，inds对应回原数组，自然要做 +1 的映射，接下来就是step-4的循环

    return keep    # 最终NMS结果返回

if __name__ == '__main__':
    dets = np.array([[100,120,170,200,0.98],
                     [20,40,80,90,0.99],
                     [20,38,82,88,0.96],
                     [200,380,282,488,0.9],
                     [19,38,75,91, 0.8]])

    py_cpu_nms(dets, 0.5)

2.2 bbox_utils.py

同样是RFBNet中的nms代码，用pytorch实现的，其实和2.1小节中的NMS操作完全一致；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
# Original author: Francisco Massa:
# https://github.com/fmassa/object-detection.torch
# Ported to PyTorch by Max deGroot (02/01/2017)
def nms(boxes, scores, overlap=0.5, top_k=200):
    """Apply non-maximum suppression at test time to avoid detecting too many
    overlapping bounding boxes for a given object. ---- 这里面有一个细节，NMS仅用于测试阶段，为什么不用于训练阶段呢？可以评论留言下，我就不解释了，嘿嘿~~~
    Args:
        boxes: (tensor) The location preds for the img, Shape: [num_priors,4].
        scores: (tensor) The class predscores for the img, Shape:[num_priors].
        overlap: (float) The overlap thresh for suppressing unnecessary boxes.
        top_k: (int) The Maximum number of box preds to consider.
    Return:
        The indices of the kept boxes with respect to num_priors.
    """

    keep = torch.Tensor(scores.size(0)).fill_(0).long()
    if boxes.numel() == 0:
        return keep
    x1 = boxes[:, 0]
    y1 = boxes[:, 1]
    x2 = boxes[:, 2]
    y2 = boxes[:, 3]
    area = torch.mul(x2 - x1, y2 - y1)    # IoU初步准备
    v, idx = scores.sort(0)  # sort in ascending order，对应step-2，不过是升序操作，非降序
    # I = I[v >= 0.01]
    idx = idx[-top_k:]  # indices of the top-k largest vals，依然是升序的结果
    xx1 = boxes.new()
    yy1 = boxes.new()
    xx2 = boxes.new()
    yy2 = boxes.new()
    w = boxes.new()
    h = boxes.new()

    # keep = torch.Tensor()
    count = 0
    while idx.numel() > 0:   # 对应step-4，若所有pred bbox都处理完毕，就可以结束循环啦~
        i = idx[-1]  # index of current largest val，top-1 score box，因为是升序的，所有返回index = -1的最后一个元素即可
        # keep.append(i)
        keep[count] = i
        count += 1    # 不仅记数NMS保留的bbox个数，也作为index存储bbox
        if idx.size(0) == 1:
            break
        idx = idx[:-1]  # remove kept element from view，top-1已保存，不需要了~~~
        # load bboxes of next highest vals
        torch.index_select(x1, 0, idx, out=xx1)
        torch.index_select(y1, 0, idx, out=yy1)
        torch.index_select(x2, 0, idx, out=xx2)
        torch.index_select(y2, 0, idx, out=yy2)
        # store element-wise max with next highest score
        xx1 = torch.clamp(xx1, min=x1[i])   # 对应 np.maximum(x1[i], x1[order[1:]]) 
        yy1 = torch.clamp(yy1, min=y1[i])
        xx2 = torch.clamp(xx2, max=x2[i])
        yy2 = torch.clamp(yy2, max=y2[i])
        w.resize_as_(xx2)
        h.resize_as_(yy2)
        w = xx2 - xx1
        h = yy2 - yy1
        # check sizes of xx1 and xx2.. after each iteration
        w = torch.clamp(w, min=0.0)    # clamp函数可以去查查，类似max、mini的操作
        h = torch.clamp(h, min=0.0)
        inter = w*h
        # IoU = i / (area(a) + area(b) - i)     
        # 以下两步操作做了个优化，area已经计算好了，就可以直接根据idx读取结果了，area[i]同理，避免了不必要的冗余计算
        rem_areas = torch.index_select(area, 0, idx)  # load remaining areas)
        union = (rem_areas - inter) + area[i]     # 就是area(a) + area(b) - i
        IoU = inter/union  # store result in iou，# IoU来啦~~~
        # keep only elements with an IoU <= overlap
        idx = idx[IoU.le(overlap)]   # 这一轮NMS操作，IoU阈值小于overlap的idx，就是需要保留的bbox，其他的就直接忽略吧，并进行下一轮计算
    return keep, count

2.2 cpu_nms.pyx

同样在RGBNet项目中，下面就是优化后的NNS操作，以及soft-NMS操作，我就不细讲了~~~

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
# --------------------------------------------------------
# Fast R-CNN
# Copyright (c) 2015 Microsoft
# Licensed under The MIT License [see LICENSE for details]
# Written by Ross Girshick
# --------------------------------------------------------

import numpy as np
cimport numpy as np

cdef inline np.float32_t max(np.float32_t a, np.float32_t b):
    return a if a >= b else b

cdef inline np.float32_t min(np.float32_t a, np.float32_t b):
    return a if a <= b else b

def cpu_nms(np.ndarray[np.float32_t, ndim=2] dets, np.float thresh):
    cdef np.ndarray[np.float32_t, ndim=1] x1 = dets[:, 0]
    cdef np.ndarray[np.float32_t, ndim=1] y1 = dets[:, 1]
    cdef np.ndarray[np.float32_t, ndim=1] x2 = dets[:, 2]
    cdef np.ndarray[np.float32_t, ndim=1] y2 = dets[:, 3]
    cdef np.ndarray[np.float32_t, ndim=1] scores = dets[:, 4]

    cdef np.ndarray[np.float32_t, ndim=1] areas = (x2 - x1 + 1) * (y2 - y1 + 1)
    cdef np.ndarray[np.int_t, ndim=1] order = scores.argsort()[::-1]

    cdef int ndets = dets.shape[0]
    cdef np.ndarray[np.int_t, ndim=1] suppressed = \
            np.zeros((ndets), dtype=np.int)

    # nominal indices
    cdef int _i, _j
    # sorted indices
    cdef int i, j
    # temp variables for box i's (the box currently under consideration)
    cdef np.float32_t ix1, iy1, ix2, iy2, iarea
    # variables for computing overlap with box j (lower scoring box)
    cdef np.float32_t xx1, yy1, xx2, yy2
    cdef np.float32_t w, h
    cdef np.float32_t inter, ovr

    keep = []
    for _i in range(ndets):
        i = order[_i]
        if suppressed[i] == 1:
            continue
        keep.append(i)
        ix1 = x1[i]
        iy1 = y1[i]
        ix2 = x2[i]
        iy2 = y2[i]
        iarea = areas[i]
        for _j in range(_i + 1, ndets):
            j = order[_j]
            if suppressed[j] == 1:
                continue
            xx1 = max(ix1, x1[j])
            yy1 = max(iy1, y1[j])
            xx2 = min(ix2, x2[j])
            yy2 = min(iy2, y2[j])
            w = max(0.0, xx2 - xx1 + 1)
            h = max(0.0, yy2 - yy1 + 1)
            inter = w * h
            ovr = inter / (iarea + areas[j] - inter)
            if ovr >= thresh:
                suppressed[j] = 1

    return keep

def cpu_soft_nms(np.ndarray[float, ndim=2] boxes, float sigma=0.5, float Nt=0.3, float threshold=0.001, unsigned int method=0):
    cdef unsigned int N = boxes.shape[0]
    cdef float iw, ih, box_area
    cdef float ua
    cdef int pos = 0
    cdef float maxscore = 0
    cdef int maxpos = 0
    cdef float x1,x2,y1,y2,tx1,tx2,ty1,ty2,ts,area,weight,ov

    for i in range(N):
        maxscore = boxes[i, 4]
        maxpos = i

        tx1 = boxes[i,0]
        ty1 = boxes[i,1]
        tx2 = boxes[i,2]
        ty2 = boxes[i,3]
        ts = boxes[i,4]

        pos = i + 1
	# get max box
        while pos < N:
            if maxscore < boxes[pos, 4]:
                maxscore = boxes[pos, 4]
                maxpos = pos
            pos = pos + 1

	# add max box as a detection 
        boxes[i,0] = boxes[maxpos,0]
        boxes[i,1] = boxes[maxpos,1]
        boxes[i,2] = boxes[maxpos,2]
        boxes[i,3] = boxes[maxpos,3]
        boxes[i,4] = boxes[maxpos,4]

	# swap ith box with position of max box
        boxes[maxpos,0] = tx1
        boxes[maxpos,1] = ty1
        boxes[maxpos,2] = tx2
        boxes[maxpos,3] = ty2
        boxes[maxpos,4] = ts

        tx1 = boxes[i,0]
        ty1 = boxes[i,1]
        tx2 = boxes[i,2]
        ty2 = boxes[i,3]
        ts = boxes[i,4]

        pos = i + 1
	# NMS iterations, note that N changes if detection boxes fall below threshold
        while pos < N:
            x1 = boxes[pos, 0]
            y1 = boxes[pos, 1]
            x2 = boxes[pos, 2]
            y2 = boxes[pos, 3]
            s = boxes[pos, 4]

            area = (x2 - x1 + 1) * (y2 - y1 + 1)
            iw = (min(tx2, x2) - max(tx1, x1) + 1)
            if iw > 0:
                ih = (min(ty2, y2) - max(ty1, y1) + 1)
                if ih > 0:
                    ua = float((tx2 - tx1 + 1) * (ty2 - ty1 + 1) + area - iw * ih)
                    ov = iw * ih / ua #iou between max box and detection box

                    if method == 1: # linear
                        if ov > Nt: 
                            weight = 1 - ov
                        else:
                            weight = 1
                    elif method == 2: # gaussian
                        weight = np.exp(-(ov * ov)/sigma)
                    else: # original NMS
                        if ov > Nt: 
                            weight = 0
                        else:
                            weight = 1

                    boxes[pos, 4] = weight*boxes[pos, 4]
		    
		    # if box score falls below threshold, discard the box by swapping with last box
		    # update N
                    if boxes[pos, 4] < threshold:
                        boxes[pos,0] = boxes[N-1, 0]
                        boxes[pos,1] = boxes[N-1, 1]
                        boxes[pos,2] = boxes[N-1, 2]
                        boxes[pos,3] = boxes[N-1, 3]
                        boxes[pos,4] = boxes[N-1, 4]
                        N = N - 1
                        pos = pos - 1

            pos = pos + 1

    keep = [i for i in range(N)]
    return keep

参考代码：

https://github.com/ruinmessi/RFBNet：RFBNet

https://github.com/rbgirshick/py-faster-rcnn：学习一百遍都不为过的faster rcnn

NMS_demo.py：https://github.com/humengdoudou/object_detection_mAP/blob/master/NMS_demo.py

参考资料

NMS及其变体

  • NMS

  • Soft-NMS

  • Softer-NMS
  • IoU-guided NMS
  • ConvNMS
  • Pure NMS
  • Yes-Net
  • LNMS
  • INMS
  • Polygon NMS
  • MNMS

参考资料

R-CNN 系列

R-CNN

  • [ ] TODO

Fast R-CNN

  • [ ] TODO

Faster R-CNN

  • [ ] TODO

Faster R-CNN 为什么用smooth l1 loss，和l2有什么区别？

SSD 算法

  • [ ] TODO

参考资料

YOLO系列（V1-V3）

YOLOV1

  • [ ] TODO

YOLOv2算法

  • [ ] TODO

YOLOv3算法

  • [ ] TODO

YOLOv1 YOLOv2 YOLOv3的发展

  • [ ] TODO

YOLOv2和YOLOv3的损失函数区别

  • [ ] TODO

参考资料

RetinaNet（Focal loss）

《Focal Loss for Dense Object Detection》

清华大学孔涛博士在知乎上这么写道：

目标的检测和定位中一个很困难的问题是，如何从数以万计的候选窗口中挑选包含目标物的物体。只有候选窗口足够多，才能保证模型的 Recall。

目前，目标检测框架主要有两种：

一种是 one-stage ，例如 YOLO、SSD 等，这一类方法速度很快，但识别精度没有 two-stage 的高，其中一个很重要的原因是，利用一个分类器很难既把负样本抑制掉，又把目标分类好。

另外一种目标检测框架是 two-stage ，以 Faster RCNN 为代表，这一类方法识别准确度和定位精度都很高，但存在着计算效率低，资源占用大的问题。

Focal Loss 从优化函数的角度上来解决这个问题，实验结果非常 solid，很赞的工作。

何恺明团队提出了用 Focal Loss 函数来训练。

因为，他在训练过程中发现，类别失衡是影响 one-stage 检测器准确度的主要原因。那么，如果能将“类别失衡”这个因素解决掉，one-stage 不就能达到比较高的识别精度了吗？

于是在研究中，何恺明团队采用 Focal Loss 函数来消除“类别失衡”这个主要障碍。

结果怎样呢？

为了评估该损失的有效性，该团队设计并训练了一个简单的密集目标检测器—RetinaNet。试验结果证明，当使用 Focal Loss 训练时，RetinaNet 不仅能赶上 one-stage 检测器的检测速度，而且还在准确度上超越了当前所有最先进的 two-stage 检测器。

参考

FPN 特征金字塔网络

  • [ ] TODO

Faster R-CNN的RPN网络

RPN结构说明：

1) 从基础网络提取的第五卷积层特征进入RPN后分为两个分支，其中一个分支进行针对feature map（上图conv-5-3共有512个feature-map）的每一个位置预测共（9*4=36）个参数，其中9代表的是每一个位置预设的9种形状的anchor-box，4对应的是每一个anchor-box的预测值（该预测值表示的是预设anchor-box到ground-truth-box之间的变换参数），上图中指向rpn-bbox-pred层的箭头上面的数字36即是代表了上述的36个参数，所以rpn-bbox-pred层的feature-map数量是36，而每一张feature-map的形状（大小）实际上跟conv5-3一模一样的；

2) 另一分支预测该anchor-box所框定的区域属于前景和背景的概率（网上很对博客说的是，指代该点属于前景背景的概率，那样是不对的，不然怎么会有18个feature-map输出呢？否则2个就足够了），前景背景的真值给定是根据当前像素（anchor-box中心）是否在ground-truth-box内；

3) 上图RPN-data(python)运算框内所进行的操作是读取图像信息（原始宽高），groun-truth boxes的信息（bounding-box的位置，形状，类别）等，作好相应的转换，输入到下面的层当中。

4) 要注意的是RPN内部有两个loss层，一个是BBox的loss,该loss通过减小ground-truth-box与预测的anchor-box之间的差异来进行参数学习，从而使RPN网络中的权重能够学习到预测box的能力。实现细节是每一个位置的anchor-box与ground-truth里面的box进行比较，选择IOU最大的一个作为该anchor-box的真值，若没有，则将之class设为背景（概率值0，否则1），这样背景的anchor-box的损失函数中每个box乘以其class的概率后就不会对bbox的损失函数造成影响。另一个loss是class-loss,该处的loss是指代的前景背景并不是实际的框中物体类别，它的存在可以使得在最后生成roi时能快速过滤掉预测值是背景的box。也可实现bbox的预测函数不受影响，使得anchor-box能（专注于）正确的学习前景框的预测，正如前所述。所以，综合来讲，整个RPN的作用就是替代了以前的selective-search方法，因为网络内的运算都是可GPU加速的，所以一下子提升了ROI生成的速度。可以将RPN理解为一个预测前景背景，并将前景框定的一个网络，并进行单独的训练，实际上论文里面就有一个分阶段训练的训练策略，实际上就是这个原因。

5) 最后经过非极大值抑制，RPN层产生的输出是一系列的ROI-data，它通过ROI的相对映射关系，将conv5-3中的特征已经存入ROI-data中，以供后面的分类网使用。

另外两个loss层的说明：
也许你注意到了，最后还有两个loss层，这里的class-loss指代的不再是前景背景loss，而是真正的类别loss了，这个应该就很好理解了。而bbox-loss则是因为rpn提取的只是前景背景的预测，往往很粗糙，这里其实是通过ROI-pooling后加上两层全连接实现更精细的box修正（这里其实是我猜的）。
ROI-Pooing的作用是为了将不同大小的Roi映射（重采样）成统一的大小输入到全连接层去。

以上。

参考资料

ROI Pooling、ROI Align和ROI Warping对比

  • [ ] TODO

参考资料

DeepLab系列（V1-V3+）

  • [ ] TODO

U-Net神经网络为什么会在医学图像分割表现好？

参考资料

Scene Parsing和Semantic Segmentation有什么不同?

参考资料

CenterNet

CornerNet介绍

CornerPooling是怎么做的？

  • [ ] TODO

TODO

  • [ ] 目标检测方向
  • [ ] 图像分割方向
  • [ ] 目标跟踪方向
  • [ ] 人脸（检测&识别&关键点）
  • [ ] OCR方向
  • [ ] SLAM方向
  • [ ] 超分辨率
  • [ ] 医疗影响方向
  • [ ] Re-ID

深度学习Tricks

Data Augmentation

由于好的深度学习模型都需要很大的数据集，所以为了加强模型的效果，在原有的数据集上，采用数据增强的方法进行数据集“扩充”，在现在的深度学习模型训练中，data augmentation几乎是必备的。

  • 常见的augmentation的方法有随机旋转、 水平/垂直翻转、随即剪裁、颜色抖动等，需要注意的是，一般旋转和剪裁是同时进行的。

    pytorch中的augmentation参考资料

  • Fancy PCA

Pre-Processing

对一个传入网络的巨大训练集来说，首先需要对数据进行预处理。

  • zero-center归一化

这种归一化对于不同的输入特征有不同的尺度(或单位)时，才有意义应用这种预处理，如果是图像(像素范围为0-255)则不用。

1
2
>>> X -= np.mean(X, axis = 0) # zero-center
>>> X /= np.std(X, axis = 0) # normalize
  • PCA Whitening
1
2
3
4
5
>>> X -= np.mean(X, axis = 0) # zero-center
>>> cov = np.dot(X.T, X) / X.shape[0] # compute the covariance matrix
>>> U,S,V = np.linalg.svd(cov) # compute the SVD factorization of the data covariance matrix
>>> Xrot = np.dot(X, U) # decorrelate the data
>>> Xwhite = Xrot / np.sqrt(S + 1e-5) # divide by the eigenvalues (which are square roots of the singular values)

这个方法的缺点是会增加数据的噪声，因为使输入具有相同的大小会延伸特征的维度。

Initialization

  • all zero initialization

如果神经元的权重初始化为相同，则它们之间就没有不对称的来源。

  • small random initialization

为了避免all zero带来的问题，并且将权重值初始化为靠近0

满足$weight \in 0.01\times N(0,1)$的高斯分布。

  • Calibrating the variance

上面的random initialization会随着输入的数量增多而方差变大，为了解决这个问题，可以将初始化权重除以输入神经元的数量

1
>>> w = np.random.randn(n) / sqrt(n) # calibrating the variances with 1/sqrt(n)

通过校准神经元的方差进行的先前初始化未考虑ReLU。专门针对ReLUs进行了初始化，得出结论，网络中神经元的方差应为

1
>>> w = np.random.randn(n) * sqrt(2.0/n) # current recommendation

During Training

  • Filters and pooling size

关于卷积核的尺寸和池化尺寸，卷积核一般采用3x3，stride=1的尺寸，可以保证特征图的输入大小不变，而池化采用的池化核尺寸为2x2。

  • Learning Rate

一般按照batch size大小来确定LR，从0.1开始，然后/2，/5进行递减，并且在固定的epoch进行decay

关于batch size的大小与LR

使用更大的batch size会导致减缓训练进度。对于凸问题，收敛速度会随着batch size的增加而降低。也就是说，在相同的epoch下，使用更大的batch size可能会导致验证集accuracy更低。

所以有一些trick来解决batch size增大的问题

  1. Linear scaling learning rate

当我们选择初始学习率为0.1，batch size为256时，那么当我们将batch size增大至b时，就需要将初始学习率增加曾0.1×b/256

  1. Learning rate warmup

选择若干个epoch进行warmup逐渐将学习率增加到指定的初始学习率

  1. Zero $\gamma $

将batch normalization的两个参数都初始化为0

  1. No bias decay

为了避免过拟合，对于权重weight和偏差bias，我们通常会使用weight decay。但在这里，仅对weight使用decay，而不对bias使用decay。

  • Fine-tune on pre-trained models

一个很好的适应新的数据集的方法是利用新的数据集在预训练的模型上进行fine-tune，需要依据新数据集的大小和与预训练数据集的相似程度来进行微调。

Activation Functions

Regularizations

Insight from Figures

Ensemble

可以将多个模型的训练结果进行融合，主要应用在比赛中

Mixup

在mixup中，每次随机采样两个样本 $(x_i,y_i)$和 $(x_2,y_2)$，然后通过加权线性插值生成新的样本进行训练

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
for i,(images,target) in enumerate(train_loader):
    # 1.input output
    images = images.cuda(non_blocking=True)
    target = torch.from_numpy(np.array(target)).float().cuda(non_blocking=True)

    # 2.mixup
    alpha=config.alpha
    lam = np.random.beta(alpha,alpha)
    index = torch.randperm(images.size(0)).cuda()
    inputs = lam*images + (1-lam)*images[index,:]
    targets_a, targets_b = target, target[index]
    outputs = model(inputs)
    loss = lam * criterion(outputs, targets_a) + (1 - lam) * criterion(outputs, targets_b)

    # 3.backward
    optimizer.zero_grad()   # reset gradient
    loss.backward()
    optimizer.step()        # update parameters of net

关于beta分布

label smoothing

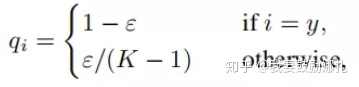
  1. 有正则化的效果
  2. Label Smoothing起到的作用实际上是抑制了feature norm，此时softmax prob不能到达$(1-\alpha)$，loss曲面上不再存在平缓区域，处处都有较大的梯度指向各个类中心，所以特征会更加聚拢。