Knowledge Distillation

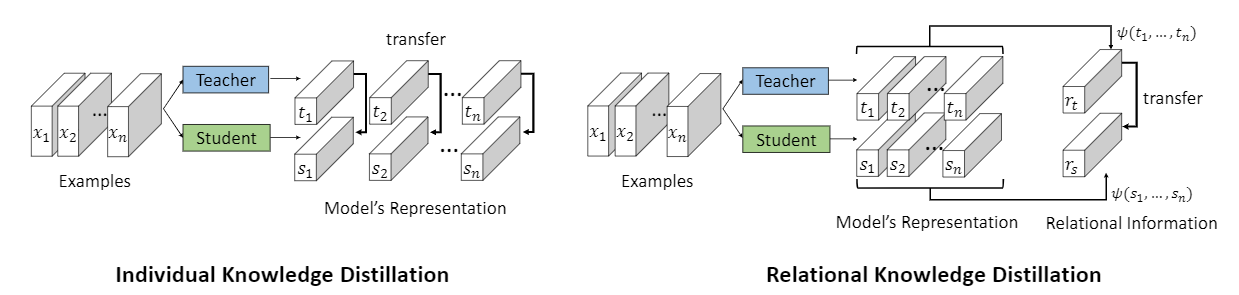
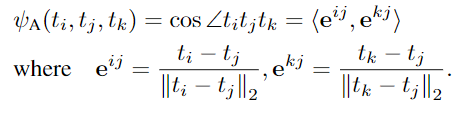知识蒸馏是一种模型压缩常见方法，用于模型压缩指的是在teacher-student框架中，将复杂、学习能力强的网络学到的特征表示“知识”蒸馏出来，传递给参数量小、学习能力弱的网络。蒸馏可以提供student在one-shot label上学不到的soft label信息，这些里面包含了类别间信息，以及student小网络学不到而teacher网络可以学到的特征表示‘知识’，所以一般可以提高student网络的精度。

本文对一些KD方法的benchmark的论文进行一些方法总结。代码分析主要来自github。

Distilling the Knowledge in a Neural Network

NIPS 2014 [https://arxiv.org/abs/1503.02531]

​ 这篇论文是知识蒸馏的开山之作，简单来说，KD就是将一个大模型(Teacher)或者多个模型的ensemble学习到的知识迁移到更轻量的模型(Student)上继续学习，从而提高student的性能。

​ 本文提出的方法是用大模型的类别概率(logits)作为”soft target”对student模型进行训练。相比于hard target，soft target包含更多的信息熵并且训练中的梯度方差会小很多，所以student模型可以用更小的数据进行训练并且收敛速度会有提升。比如MNIST任务中，２看起来可能会像3/7会有信息包含在soft target中，但是经过softmax之后会接近于0，丢失一些信息。

​ 作者使用logits(最后一个softmax之前的输入)作为student模型的学习目标，即将teacher的logits和student的logits平方差最小化。在文中作者作者提出了Softmax_T

$$q_i = \frac{exp(z_i/T)}{\sum_jexp(z_j/T)}$$

​ 如果将T取1，这个公式就是softmax，根据logit输出各个类别的概率。如果T接近于0，则最大的值会越近1，其它值会接近0，近似于onehot编码。如果T越大，则输出的结果的分布越平缓，相当于平滑的一个作用，可以是概率分布更集中，起到保留相似信息的作用。如果T等于无穷，就是一个均匀分布。

​ 在蒸馏任务中，一般采用两个损失函数，第一个是和soft-target的cross-entropy，第二个是和正确label的cross-entropy，但一般第二个损失函数需要设置一个较低的权重。

​ 经过简化的目标函数为

$$\frac{\delta C}{\delta z_i} = \frac{1}{NT^2}(z_i-v_i)$$

其中vi是大模型有温度的softmax输出，zi是小模型有温度的softmax输出。

代码

class DistillKL(nn.Module):
    """Distilling the Knowledge in a Neural Network"""
    def __init__(self, T):
        super(DistillKL, self).__init__()
        self.T = T

    def forward(self, y_s, y_t):
        p_s = F.log_softmax(y_s/self.T, dim=1)
        p_t = F.softmax(y_t/self.T, dim=1)
        loss = F.kl_div(p_s, p_t, size_average=False) * (self.T**2) / y_s.shape[0]
        return loss

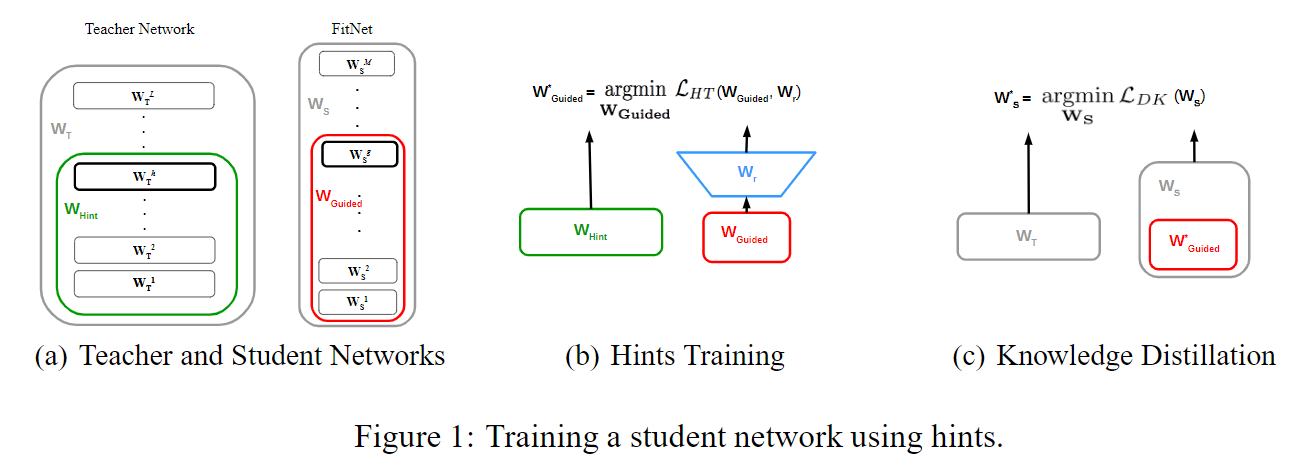
FITNETS: HINTS FOR THIN DEEP NETS

ICLR2015 [https://arxiv.org/abs/1412.6550]

​ 本文指出之前的工作都是利用student或者一组模型的ensemble压缩为深度宽度相·当或者较浅和较宽的student网络，没有有效的利用深度。

​ 文章提出了FitNets方法去压缩较宽和较深的网络，即student网络为thiner and deeper Network(比teacher更深)。主要方法是用teacher的中间隐藏层引导student网络进行学习，期望student网络能够学习一个中间的表现形式能够对teacher网络的中间层进行预测。

​ 实现

​ 选取teacher网络中间的隐藏层作为hint layer，同样选取student网络中间的隐藏层作为guide layer向hintt layer学习。

$$L_{HT}(W_{Guided}, W_r) = 1/2||u_h(X;W_{Hint}-r(v_g(X;W_{Guided});Wr)||^2$$

​ 训练策略

​ teacher网络的前 $h$层作为$W_{Hint}$ ，student网络的前$g$层作为 $W_{Guided}$,$W_{Hint}$指导$W_{Guided}$训练，然后初始化$W_r$适配层的参数。

​ 第一阶段用teacher网络的hint层预训练student网络的guided层

​ 第二阶段是对整个网络做知识蒸馏

​ 代码实现

class HintLoss(nn.Module):
    """Fitnets: hints for thin deep nets, ICLR 2015"""
    def __init__(self):
        super(HintLoss, self).__init__()
        self.crit = nn.MSELoss()

    def forward(self, f_s, f_t):
        loss = self.crit(f_s, f_t)
        return loss

Paying More Attention to Attention: Improving the Performance of Convolutional Neural Networks via Attention Transfer

ICLR 2017[https://arxiv.org/abs/1612.03928]

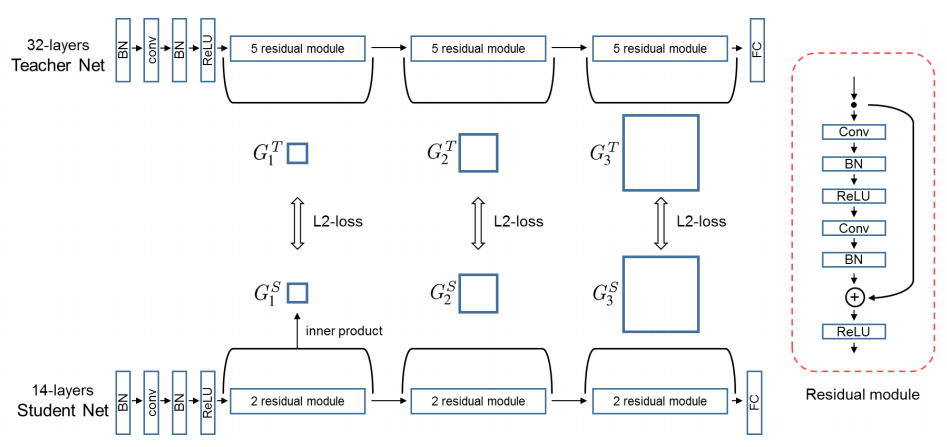
Attention Transfer传递了teacher网络的attention信息给student网络，CNN的attention一般分为两种，spatial-attention,channel-attention。本文利用的是spatial-attention.所谓spatial-attention即一种热力图，用来解码出输入图像空间区域对输出贡献大小。文章提出了两种可利用的spatial-attention,基于响应图的和基于梯度图的。

activation-based AT

基于特征图取出某层输出特征图张量A，定义一个映射F:

$$F:R^{CXHXW->R^{HXW}}$$

文中提出了三种映射方式：

1. 各通道绝对值相加$F_{sum}(A) = \sum^C_{i=1}|A_i|$
2. 各通道绝对值p次幂相加$F_{sum}^p(A) =\sum^C_{i=1}|A_i|^p$
3. 各通道绝对值p次幂最大值$F_{max}^p(A)=max_{i=1,C}|A_i|^p$

不同level的attention map的activation在不同的位置，由浅到深从眼睛到眼睛鼻子再到全脸。

​ 网络的架构

$$L_{AT} = L(W_S, x) + \frac{\beta}{2}\sum_{j\epsilon x}||\frac{Q_S^j}{||Q_S^j||_2}-\frac{Q_T^j}{||Q_T^j||_2}||_p$$

gradient-based AT

代码实现

class Attention(nn.Module):
    """Paying More Attention to Attention: Improving the Performance of Convolutional Neural Networks
    via Attention Transfer
    code: https://github.com/szagoruyko/attention-transfer"""
    def __init__(self, p=2):
        super(Attention, self).__init__()
        self.p = p

    def forward(self, g_s, g_t):
        return [self.at_loss(f_s, f_t) for f_s, f_t in zip(g_s, g_t)]

    def at_loss(self, f_s, f_t):
        s_H, t_H = f_s.shape[2], f_t.shape[2]
        if s_H > t_H:
            f_s = F.adaptive_avg_pool2d(f_s, (t_H, t_H))
        elif s_H < t_H:
            f_t = F.adaptive_avg_pool2d(f_t, (s_H, s_H))
        else:
            pass
        return (self.at(f_s) - self.at(f_t)).pow(2).mean()

    def at(self, f):
        return F.normalize(f.pow(self.p).mean(1).view(f.size(0), -1))

A Gift from Knowledge Distillation: Fast Optimization, Network Minimization and Transfer Learning

CVPR 2017[https://openaccess.thecvf.com/content_cvpr_2017/papers/Yim_A_Gift_From_CVPR_2017_paper.pdf]

这篇文章的蒸馏方法不是通过Teacher直接输出的feature map作为student网络的训练目标，而是将teacher网络层间的关系作为student网络学习的target。

FSP Metrix

文章提出的描述层与层之间关系的方法FSP matrix，是某层特征图与另外一层特征图之间的偏心协方差矩阵（即没有减去均值的协方差矩阵）。如F1层特征图配置（H,W,M）M为通道数。F2层特征图配置（H,W,N）。得到一个M * N的矩阵G。G（i，j）为F1第i通道与F2第j通道的elemet-wise乘积之和：

$$G_{i,j}(x;W) = \sum^h_{s=1}\sum^w_{t=1}\frac{F^1_{s,t,i}(x;W)*F^2_{s,t,j}(x;W)}{h*w}$$

网络结构

最后的loss

$$L_{FSP}(W_t,W_s) = \frac{1}{N}\sum_x\sum^n_{i=1}\lambda_i*||G_i^T(x;W_t)-G_i^S(x;W_a)||_2^2$$

代码实现

class FSP(nn.Module):
    """A Gift from Knowledge Distillation:
    Fast Optimization, Network Minimization and Transfer Learning"""
    def __init__(self, s_shapes, t_shapes):
        super(FSP, self).__init__()
        assert len(s_shapes) == len(t_shapes), 'unequal length of feat list'
        s_c = [s[1] for s in s_shapes]
        t_c = [t[1] for t in t_shapes]
        if np.any(np.asarray(s_c) != np.asarray(t_c)):
            raise ValueError('num of channels not equal (error in FSP)')

    def forward(self, g_s, g_t):
        s_fsp = self.compute_fsp(g_s)
        t_fsp = self.compute_fsp(g_t)
        loss_group = [self.compute_loss(s, t) for s, t in zip(s_fsp, t_fsp)]
        return loss_group

    @staticmethod
    def compute_loss(s, t):
        return (s - t).pow(2).mean()

    @staticmethod
    def compute_fsp(g):
        fsp_list = []
        for i in range(len(g) - 1):
            bot, top = g[i], g[i + 1]
            b_H, t_H = bot.shape[2], top.shape[2]
            if b_H > t_H:
                bot = F.adaptive_avg_pool2d(bot, (t_H, t_H))
            elif b_H < t_H:
                top = F.adaptive_avg_pool2d(top, (b_H, b_H))
            else:
                pass
            bot = bot.unsqueeze(1)
            top = top.unsqueeze(2)
            bot = bot.view(bot.shape[0], bot.shape[1], bot.shape[2], -1)
            top = top.view(top.shape[0], top.shape[1], top.shape[2], -1)

            fsp = (bot * top).mean(-1)
            fsp_list.append(fsp)
        return fsp_list

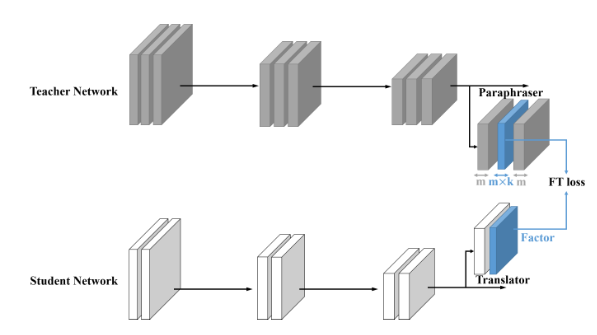
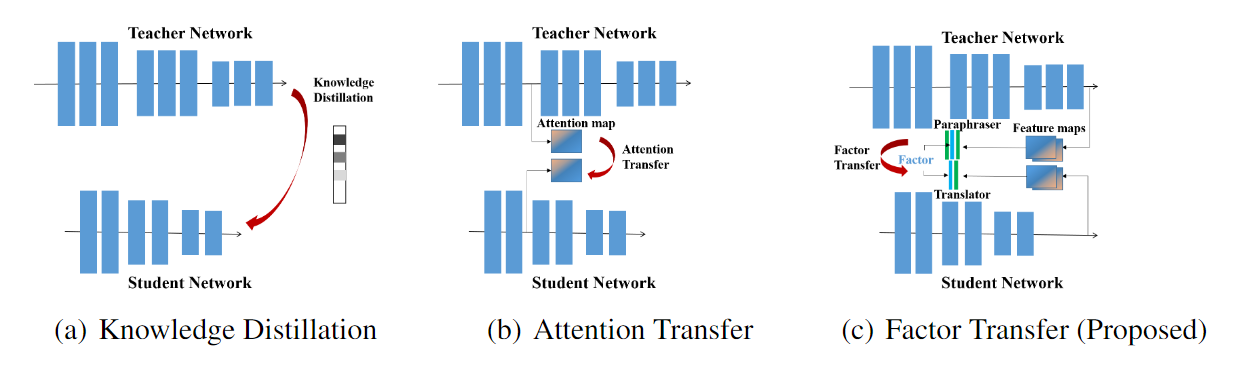
Paraphrasing Complex Network: Network Compression via Factor Transfer

NIPS 2018[https://arxiv.org/abs/1802.04977]

这篇文章提出了两个卷积模块，释义器(paraphrarer)和翻译器(traslator)。释义器由无监督方法训练，用于提取Teacher网络中的因子作为Teacher网络中的信息，翻译器用于提取student网络中的因子并且对Teacher中的因子进行翻译学习。

网络架构

文章提出，例如KD，AT等蒸馏方法虽然可以有很好的知识传递效果，但是忽略了Teacher网络和Student网络中的比如网络架构，通道数量，初始化条件等因素。在文章中，提出的架构拥有一个释义器将Teacher 的特征进行解释，可以让Student更好的学习知识。总结如下：

• 用无监督的方式训练一个teacher网络的释义器。
• student通过卷积化的翻译器对teacher释义的因子进行学习

Teacher无监督paraphraser

$$Lrec=‖x−P(x)‖2$$

用输入的特征图与释义器输出的释义信息P(x)进行损失计算用于无监督的训练paraphraser。如果网络输出的为m通道特征，则将释义器释义的特征通道设置为mxk，k为释义系数。

Student translator — Factor Transfer

translator作为一个“缓冲区”来学习Teacher提供的Factor信息。

具体的Loss如下

$$Lstudent=Lcls+βLF T\\ Lcls=C(S(Ix),y)\\ LF T=‖\frac{FT}{‖FT‖^2}−\frac{FS}{‖FS‖^2}‖_p$$

代码实现

class FactorTransfer(nn.Module):
    """Paraphrasing Complex Network: Network Compression via Factor Transfer, NeurIPS 2018"""
    def __init__(self, p1=2, p2=1):
        super(FactorTransfer, self).__init__()
        self.p1 = p1
        self.p2 = p2

    def forward(self, f_s, f_t):
        return self.factor_loss(f_s, f_t)

    def factor_loss(self, f_s, f_t):
        s_H, t_H = f_s.shape[2], f_t.shape[2]
        if s_H > t_H:
            f_s = F.adaptive_avg_pool2d(f_s, (t_H, t_H))
        elif s_H < t_H:
            f_t = F.adaptive_avg_pool2d(f_t, (s_H, s_H))
        else:
            pass
        if self.p2 == 1:
            return (self.factor(f_s) - self.factor(f_t)).abs().mean()
        else:
            return (self.factor(f_s) - self.factor(f_t)).pow(self.p2).mean()

    def factor(self, f):
        return F.normalize(f.pow(self.p1).mean(1).view(f.size(0), -1))

Learning Deep Representations with Probabilistic Knowledge Transfer

ECCV 2018[https://arxiv.org/abs/1803.10837]

这篇文章提出了一种KT方法，通过匹配特征在空间中的概率分布来进行知识迁移，而不是使用实际的特征表示。

由于一般的KT方法都是用classification的layer来进行知识迁移，输出的特征图无论网络的架构大小size都是固定的，所以普通的KT不适用于一些其他的任务。还有一点是一般的KT网络都忽略了样本之间的相似性，特征的空间几何形状等信息。

本文提出的概率知识转移方法：

TODO

Knowledge Transfer via Distillation of Activation Boundaries Formed by Hidden Neurons

AAAI 2019[https://arxiv.org/abs/1811.03233]

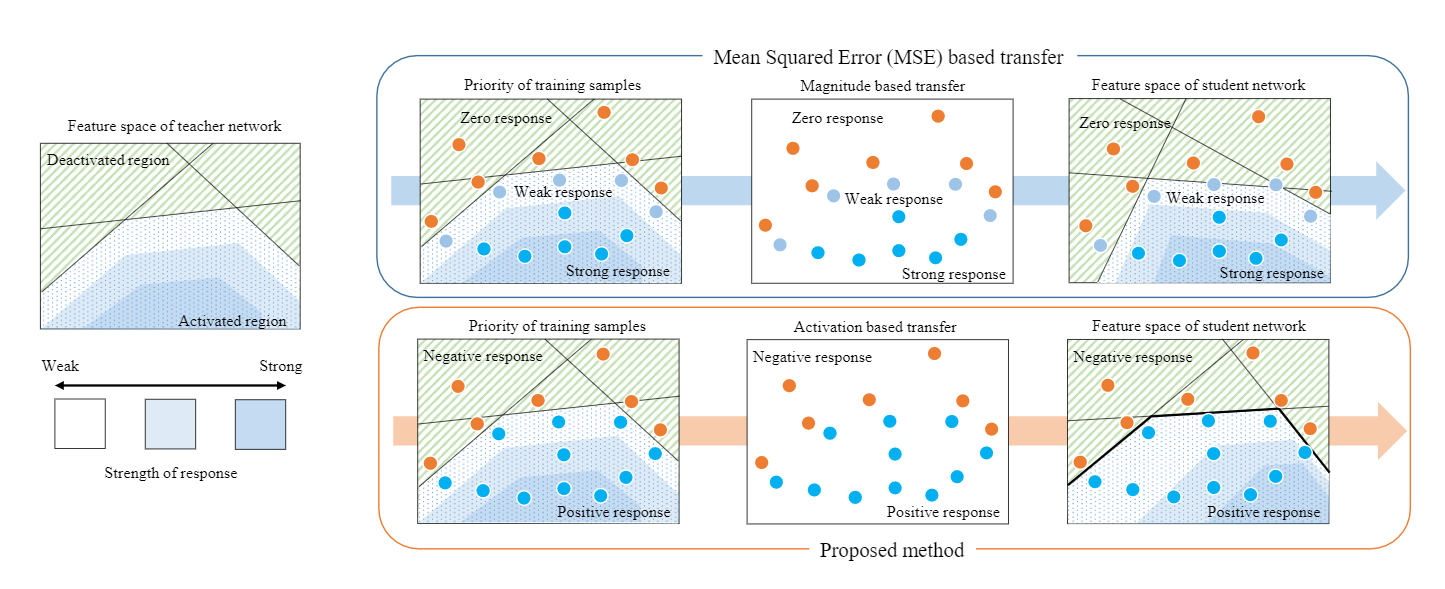
文章提出了一种通过隐藏神经元形成的激活边界蒸馏的知识转移方法。student网络学习teacher网络神经元的激活区域和非激活区域的分离边界。运用激活转移损失来最小化Teacher和Student网络之间的神经元激活差异，这个损失考虑的不是神经元的反应强度以及数值特征，而是考虑神经元是否被激活。但是激活函数不可微所以文中提出了替代损失和激活转移损失近似来训练。

一般的方法是对RELU之后的特征图进行迁移学习,只能反映激活的程度,而这篇文章提出的方法是考虑神经元是否激活,如下图所示.

MSE based

$$L(I) = ||\sigma(T(I))-\sigma(S(I))||^2_2$$

Proposed

$$consider \ whether \ neuron \ is \ activated\\ p(x) = \begin{cases}1, \ if \ x>0 \\ 0, \ other wise\end{cases}\\ loss\\ L(I) = ||p(T(I))-p(S(I))||_1$$

但是上面公式是不可微的,所以提出一种近似的可微形式

$$L(I) =‖ρ(T(I))σ(μ1−r(S(I)))+ (1−ρ(T(I)))σ(μ1+r(S(I)))‖^2_2$$

r代表将student的向量转换为teacher的大小.

对于卷积层

$$L(I) =\sum^H_i\sum^W_j‖ρ(T(I)ij)σ(μ1−r(S(I)ij))+ (1−ρ(T(I)ij))σ(μ1+r(S(I)ij))‖^2_2$$

将HXW特征图每个点(1x1xM)作为计算的vector

代码实现

class ABLoss(nn.Module):
    """Knowledge Transfer via Distillation of Activation Boundaries Formed by Hidden Neurons
    code: https://github.com/bhheo/AB_distillation
    """
    def __init__(self, feat_num, margin=1.0):
        super(ABLoss, self).__init__()
        self.w = [2**(i-feat_num+1) for i in range(feat_num)]
        self.margin = margin

    def forward(self, g_s, g_t):
        bsz = g_s[0].shape[0]
        losses = [self.criterion_alternative_l2(s, t) for s, t in zip(g_s, g_t)]
        losses = [w * l for w, l in zip(self.w, losses)]
        # loss = sum(losses) / bsz
        # loss = loss / 1000 * 3
        losses = [l / bsz for l in losses]
        losses = [l / 1000 * 3 for l in losses]
        return losses

    def criterion_alternative_l2(self, source, target):
        loss = ((source + self.margin) ** 2 * ((source > -self.margin) & (target <= 0)).float() +
                (source - self.margin) ** 2 * ((source <= self.margin) & (target > 0)).float())
        return torch.abs(loss).sum()

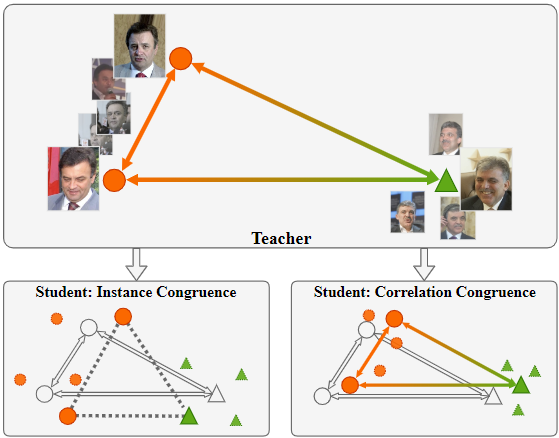
Correlation Congruence for Knowledge Distillation

ICCV 2019[https://arxiv.org/abs/1904.01802]

文章提出了一种方法不仅可以在distillation中进行实例级信息传递，并且可以对实例之间的相关性进行传递。提出了一种基于内核的方法以及采样策略能够在一个mini-batch中找到实例的一致性。

具体结构

1. 实例一致性(student和teacher预测的KL散度)
2. 相关一致性(student和teacher相关性的欧式距离)

$$特征F_t \ F_s \\F_t = matrix(f_1^t,f_2^t,...,f_n^t) \\F_s = matrix(f_1^s,f_2^s,...,f_n^s) \\C代表相关性矩阵, \phi代表相关性运算 \\C_{ij} = \phi(f_i,f_j) \\correlation congruence \ LOSS \\L_{CC} = \frac{1}{n^2}||\psi(F_t)-\psi(F_s)||_2^2 \\=\frac{1}{n^2}\sum_{i,j}(\phi(f_i^s,f_j^s)-\phi(f_i^t,f_j^t))^2 \\总Loss \\L_{KKCD} = \alpha L_{CE} + (1-\alpha)L_{KD}+\beta L_{CC}$$

• kernel-based相关性计算

• Mini-batch采样策略

TODO

代码实现

class CC(nn.Module):
	'''
	Correlation Congruence for Knowledge Distillation
	http://openaccess.thecvf.com/content_ICCV_2019/papers/
	Peng_Correlation_Congruence_for_Knowledge_Distillation_ICCV_2019_paper.pdf
	'''
	def __init__(self, gamma, P_order):
		super(CC, self).__init__()
		self.gamma = gamma
		self.P_order = P_order

	def forward(self, feat_s, feat_t):
		corr_mat_s = self.get_correlation_matrix(feat_s)
		corr_mat_t = self.get_correlation_matrix(feat_t)

		loss = F.mse_loss(corr_mat_s, corr_mat_t)

		return loss

	def get_correlation_matrix(self, feat):
		feat = F.normalize(feat, p=2, dim=-1)
		sim_mat  = torch.matmul(feat, feat.t())
		corr_mat = torch.zeros_like(sim_mat)

		for p in range(self.P_order+1):
			corr_mat += math.exp(-2*self.gamma) * (2*self.gamma)**p / \
						math.factorial(p) * torch.pow(sim_mat, p)

		return corr_mat

like what you like: knowledge distill via neuron selectivity transfer

ICLR 2019[https://arxiv.org/abs/1707.01219]

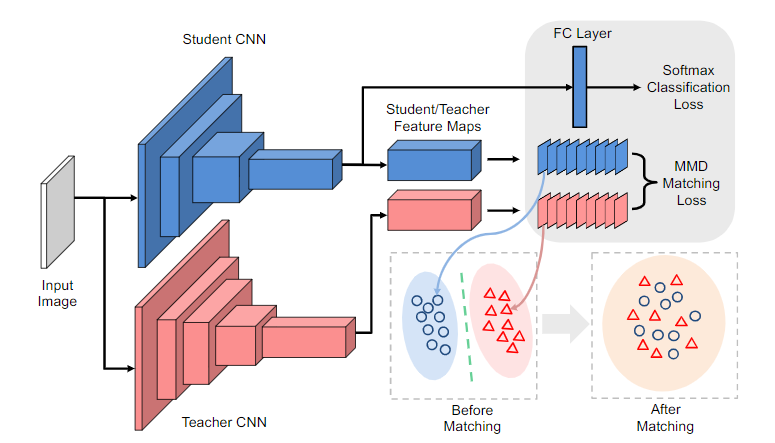
这篇文章提出了一种新的KT方法,通过匹配Teacher和student网络中的神经元选择模式的分布来进行知识迁移.

Maximum Mean Discrepancy

$$L_{NST}(W_S) = H(y_{true}, P_S)+\frac{\lambda}{2}L_{MMD^2}(F_T,F_S)$$

Choice of Kernels

• Linear Kernel: $k(x,y) = x^Ty$
• Polynomial Kernel:$k(x,y) = (x^Ty+c)^d$ d=2 ,c=0
• Gaussian Kernel: $k(x,y) = exp(-\frac{||x-y||^2_2}{2\sigma^2}) \ \sigma^2是平方距离$

TODO

代码实现

class NSTLoss(nn.Module):
    """like what you like: knowledge distill via neuron selectivity transfer"""
    def __init__(self):
        super(NSTLoss, self).__init__()
        pass

    def forward(self, g_s, g_t):
        return [self.nst_loss(f_s, f_t) for f_s, f_t in zip(g_s, g_t)]

    def nst_loss(self, f_s, f_t):
        s_H, t_H = f_s.shape[2], f_t.shape[2]
        if s_H > t_H:
            f_s = F.adaptive_avg_pool2d(f_s, (t_H, t_H))
        elif s_H < t_H:
            f_t = F.adaptive_avg_pool2d(f_t, (s_H, s_H))
        else:
            pass

        f_s = f_s.view(f_s.shape[0], f_s.shape[1], -1)
        f_s = F.normalize(f_s, dim=2)
        f_t = f_t.view(f_t.shape[0], f_t.shape[1], -1)
        f_t = F.normalize(f_t, dim=2)

        # set full_loss as False to avoid unnecessary computation
        full_loss = True
        if full_loss:
            return (self.poly_kernel(f_t, f_t).mean().detach() + self.poly_kernel(f_s, f_s).mean()
                    - 2 * self.poly_kernel(f_s, f_t).mean())#detach在当前计算图中剥离variable并不求其梯度
        else:
            return self.poly_kernel(f_s, f_s).mean() - 2 * self.poly_kernel(f_s, f_t).mean()

    def poly_kernel(self, a, b):
        a = a.unsqueeze(1)
        b = b.unsqueeze(2)
        res = (a * b).sum(-1).pow(2)
        return res

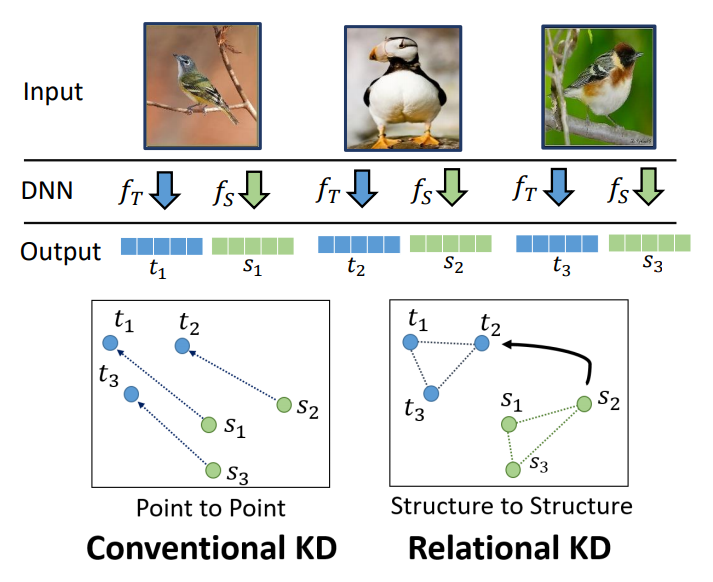
Relational Knowledge Disitllation

CVPR 2019[https://arxiv.org/abs/1904.05068]

文章提出了一种基于关系的知识蒸馏方法.作者认为知识的表达用结构关系比单独的实例来表达更好.

文章提出了两种关系知识蒸馏方法,基于距离和基于角度的方法.

$$L_{RKD} = \sum_{(x_1,...,x_n)\in \chi^N}l(\psi(t_1,..,t_n),\psi(s_1,...,s_n))$$

即用特征的n元组的关系进行知识迁移.ψ是关系势函数.不管teacher网络的尺寸和student是否匹配,都可以通过关系势函数进行高阶的知识迁移.

Distance-wise(二元组)

$$\psi_D(t_i,t_j) = \frac{1}{\mu}||t_i-t_j||_2 \\μ是基于距离的归一化因子 \\\mu = \frac{1}{|\chi^2|}\sum_{(x_i,x_j)\in\chi^2}||t_i-t_j||_2 \\L_{RKD-D}=\sum_{(xi,xj)∈\chi^2}l_δ(ψ_D(t_i,t_j),ψ_D(s_i,s_j)) \\l_δ=\begin{cases}\frac{1}{2}(x-y)^2, \ \ for|x-y|<=1\\|x-y|-\frac{1}{2}, \ otherwise\end{cases}$$

这种方法不会强制student网络去匹配teacher的logits,而是匹配teacher的距离结构.

Angle-wise(三元组)

代码实现

class RKDLoss(nn.Module):
    """Relational Knowledge Disitllation, CVPR2019"""
    def __init__(self, w_d=25, w_a=50):
        super(RKDLoss, self).__init__()
        self.w_d = w_d
        self.w_a = w_a

    def forward(self, f_s, f_t):
        student = f_s.view(f_s.shape[0], -1)
        teacher = f_t.view(f_t.shape[0], -1)

        # RKD distance loss
        with torch.no_grad():
            t_d = self.pdist(teacher, squared=False)
            mean_td = t_d[t_d > 0].mean()
            t_d = t_d / mean_td

        d = self.pdist(student, squared=False)
        mean_d = d[d > 0].mean()
        d = d / mean_d

        loss_d = F.smooth_l1_loss(d, t_d)

        # RKD Angle loss
        with torch.no_grad():
            td = (teacher.unsqueeze(0) - teacher.unsqueeze(1))
            norm_td = F.normalize(td, p=2, dim=2)
            t_angle = torch.bmm(norm_td, norm_td.transpose(1, 2)).view(-1)

        sd = (student.unsqueeze(0) - student.unsqueeze(1))
        norm_sd = F.normalize(sd, p=2, dim=2)
        s_angle = torch.bmm(norm_sd, norm_sd.transpose(1, 2)).view(-1)

        loss_a = F.smooth_l1_loss(s_angle, t_angle)

        loss = self.w_d * loss_d + self.w_a * loss_a

        return loss

    @staticmethod
    def pdist(e, squared=False, eps=1e-12):
        e_square = e.pow(2).sum(dim=1)
        prod = e @ e.t()
        res = (e_square.unsqueeze(1) + e_square.unsqueeze(0) - 2 * prod).clamp(min=eps)

        if not squared:
            res = res.sqrt()

        res = res.clone()
        res[range(len(e)), range(len(e))] = 0
        return res

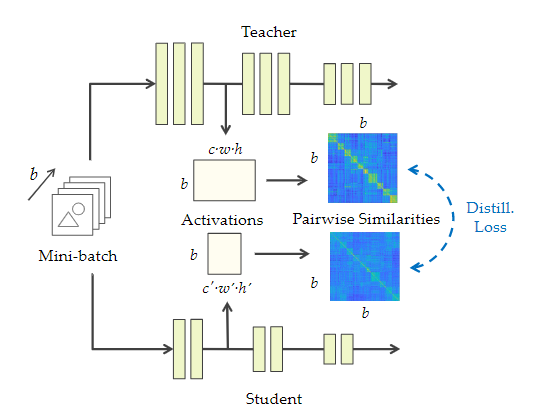
Similarity-Preserving Knowledge Distillation

ICCV 2019[https://arxiv.org/abs/1907.09682]

文章提出了一种新的蒸馏损失,利用输入的相似性会有相似的激活模式,student网络不用模仿teacher的表征空间,在自己的特征空间中保持相对性.

QT是特征的reshape,大小为(b,chw),所以G大小为(b,b)

损失函数为

$$L_{SP}(G_T,G_S) =\frac{1}{b^2}\sum_{(l,l′)∈I}||G(l)_T−G(l′)_S||^2_F$$

l,l’是相同depth的层的特征或者block输出层的特征.

代码实现

class Similarity(nn.Module):
    """Similarity-Preserving Knowledge Distillation, ICCV2019, verified by original author"""
    def __init__(self):
        super(Similarity, self).__init__()

    def forward(self, g_s, g_t):
        return [self.similarity_loss(f_s, f_t) for f_s, f_t in zip(g_s, g_t)]

    def similarity_loss(self, f_s, f_t):
        bsz = f_s.shape[0]
        f_s = f_s.view(bsz, -1)
        f_t = f_t.view(bsz, -1)

        G_s = torch.mm(f_s, torch.t(f_s))
        # G_s = G_s / G_s.norm(2)
        G_s = torch.nn.functional.normalize(G_s)
        G_t = torch.mm(f_t, torch.t(f_t))
        # G_t = G_t / G_t.norm(2)
        G_t = torch.nn.functional.normalize(G_t)

        G_diff = G_t - G_s
        loss = (G_diff * G_diff).view(-1, 1).sum(0) / (bsz * bsz)
        return loss

Variational Information Distillation for Knowledge Transfer

CVPR 2019[https://arxiv.org/abs/1904.05835]

文章提出了一种基于信息理论的蒸馏方法，采用变分信息最大化方法将知识迁移公式化为最大化teacher和student网络之间的相互信息。

$$I(t;s) = H(t)-H(t|s) \\=-E_t[log \ p(t)]+E_t,s[log \ p(t|s)]$$

互信息为[教师模型的熵值] - [已知学生模型的条件下的教师模型熵值]当学生模型已知，能够使得教师模型的熵很小，这说明学生模型以及获得了能够恢复教师模型所需要的“压缩”知识，间接说明了此时学生模型已经学习的很好了。而这种情况下也就是说明上述公式中的H(t|s)很小，从而使得互信息I(t;s)会很大。作者从这个角度解释了为什么可以通过最大化互信息的方式来进行蒸馏学习。

TODO

代码实现

class VIDLoss(nn.Module):
    """Variational Information Distillation for Knowledge Transfer (CVPR 2019),
    code from author: https://github.com/ssahn0215/variational-information-distillation"""
    def __init__(self,
                 num_input_channels,
                 num_mid_channel,
                 num_target_channels,
                 init_pred_var=5.0,
                 eps=1e-5):
        super(VIDLoss, self).__init__()

        def conv1x1(in_channels, out_channels, stride=1):
            return nn.Conv2d(
                in_channels, out_channels,
                kernel_size=1, padding=0,
                bias=False, stride=stride)

        self.regressor = nn.Sequential(
            conv1x1(num_input_channels, num_mid_channel),
            nn.ReLU(),
            conv1x1(num_mid_channel, num_mid_channel),
            nn.ReLU(),
            conv1x1(num_mid_channel, num_target_channels),
        )
        self.log_scale = torch.nn.Parameter(
            np.log(np.exp(init_pred_var-eps)-1.0) * torch.ones(num_target_channels)
            )
        self.eps = eps

    def forward(self, input, target):
        # pool for dimentsion match
        s_H, t_H = input.shape[2], target.shape[2]
        if s_H > t_H:
            input = F.adaptive_avg_pool2d(input, (t_H, t_H))
        elif s_H < t_H:
            target = F.adaptive_avg_pool2d(target, (s_H, s_H))
        else:
            pass
        pred_mean = self.regressor(input)
        pred_var = torch.log(1.0+torch.exp(self.log_scale))+self.eps
        pred_var = pred_var.view(1, -1, 1, 1)
        neg_log_prob = 0.5*(
            (pred_mean-target)**2/pred_var+torch.log(pred_var)
            )
        loss = torch.mean(neg_log_prob)
        return loss

总结

1.Logits(Response)-based

• Distilling the Knowledge in a Neural Network

2.Feature-based

• FITNETS: HINTS FOR THIN DEEP NETS
• Paying More Attention to Attention: Improving the Performance of Convolutional Neural Networks via Attention Transfer
• Paraphrasing Complex Network: Network Compression via Factor Transfer
• Knowledge Transfer via Distillation of Activation Boundaries Formed by Hidden Neurons
• like what you like: knowledge distill via neuron selectivity transfer

3.Relation-based

• A Gift from Knowledge Distillation: Fast Optimization, Network Minimization and Transfer Learning
• Learning Deep Representations with Probabilistic Knowledge Transfer
• Correlation Congruence for Knowledge Distillation
• Relational Knowledge Disitllation
• Similarity-Preserving Knowledge Distillation
• Variational Information Distillation for Knowledge Transfer